Document

lstsq(a, b, rcond='warn')

Computes the vector x that approximately solves the equation a @ x = b . The equation may be under-, well-, or over-determined (i.e., the number of linearly independent rows of a can be less than, equal to, or greater than its number of linearly independent columns). If a is square and of full rank, then x (but for round-off error) is the "exact" solution of the equation. Else, x minimizes the Euclidean 2-norm $||b - ax||$ . If there are multiple minimizing solutions, the one with the smallest 2-norm $||x||$ is returned.

Notes

If b is a matrix, then all array results are returned as matrices.

Parameters

a : (M, N) array_like: "Coefficient" matrix.
b : {(M,), (M, K)} array_like: Ordinate or "dependent variable" values. If b is two-dimensional, the least-squares solution is calculated for each of the K columns of b.
rcond : float, optional: Cut-off ratio for small singular values of a. For the purposes of rank determination, singular values are treated as zero if they are smaller than :None:None:`rcond` times the largest singular value of a.

versionchanged

If not set, a FutureWarning is given. The previous default of -1 will use the machine precision as :None:None:`rcond` parameter, the new default will use the machine precision times :None:None:`max(M, N)`. To silence the warning and use the new default, use rcond=None , to keep using the old behavior, use rcond=-1 .

Raises

LinAlgError: If computation does not converge.

Returns

x : {(N,), (N, K)} ndarray: Least-squares solution. If b is two-dimensional, the solutions are in the K columns of x.
residuals : {(1,), (K,), (0,)} ndarray: Sums of squared residuals: Squared Euclidean 2-norm for each column in b - a @ x . If the rank of a is < N or M <= N, this is an empty array. If b is 1-dimensional, this is a (1,) shape array. Otherwise the shape is (K,).
rank : int: Rank of matrix a.
s : (min(M, N),) ndarray: Singular values of a.

Return the least-squares solution to a linear matrix equation.

Examples

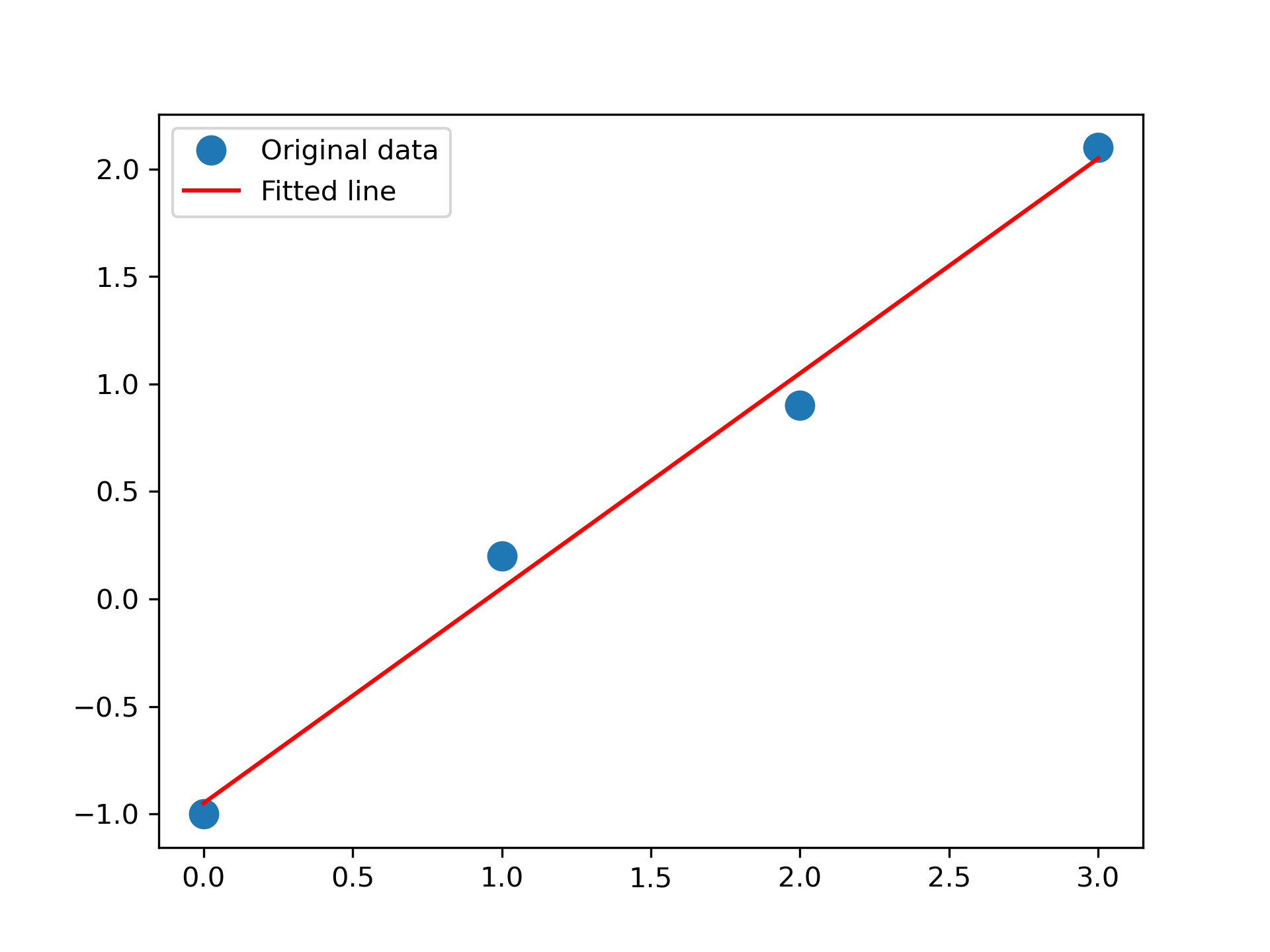
Fit a line, y = mx + c , through some noisy data-points:

>>> x = np.array([0, 1, 2, 3])
... y = np.array([-1, 0.2, 0.9, 2.1])

By examining the coefficients, we see that the line should have a gradient of roughly 1 and cut the y-axis at, more or less, -1.

We can rewrite the line equation as y = Ap , where A = [[x 1]] and p = [[m], [c]] . Now use lstsq to solve for :None:None:`p`:

>>> A = np.vstack([x, np.ones(len(x))]).T
... A
array([[ 0.,  1.],
       [ 1.,  1.],
       [ 2.,  1.],
       [ 3.,  1.]])

>>> m, c = np.linalg.lstsq(A, y, rcond=None)[0]
... m, c
(1.0 -0.95) # may vary

Plot the data along with the fitted line:

>>> import matplotlib.pyplot as plt
... _ = plt.plot(x, y, 'o', label='Original data', markersize=10)
... _ = plt.plot(x, m*x + c, 'r', label='Fitted line')
... _ = plt.legend()
... plt.show()

See :

Back References

The following pages refer to to this document either explicitly or contain code examples using this.

numpy.polynomial.polynomial.polyfit numpy.ma.extras.polyfit numpy.polynomial.hermite_e.hermefit numpy.linalg.qr numpy.polyfit numpy.polynomial.chebyshev.chebfit numpy.linalg.solve numpy.polynomial.hermite.hermfit numpy.polynomial.legendre.legfit numpy.polynomial.laguerre.lagfit numpy.linalg.lstsq

Local connectivity graph

Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.

Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)

SVG is more flexible but power hungry; and does not scale well to 50 + nodes.

All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them

GitHub : /numpy/linalg/linalg.py#2157
type: <class 'function'>
Commit: