Document

blackman(M)

The Blackman window is a taper formed by using the first three terms of a summation of cosines. It was designed to have close to the minimal leakage possible. It is close to optimal, only slightly worse than a Kaiser window.

Notes

The Blackman window is defined as

$$w(n) = 0.42 - 0.5 \cos(2\pi n/M) + 0.08 \cos(4\pi n/M)$$

Most references to the Blackman window come from the signal processing literature, where it is used as one of many windowing functions for smoothing values. It is also known as an apodization (which means "removing the foot", i.e. smoothing discontinuities at the beginning and end of the sampled signal) or tapering function. It is known as a "near optimal" tapering function, almost as good (by some measures) as the kaiser window.

Parameters

M : int: Number of points in the output window. If zero or less, an empty array is returned.

Returns

out : ndarray: The window, with the maximum value normalized to one (the value one appears only if the number of samples is odd).

Return the Blackman window.

Examples

>>> import matplotlib.pyplot as plt
... np.blackman(12)
array([-1.38777878e-17,   3.26064346e-02,   1.59903635e-01, # may vary
        4.14397981e-01,   7.36045180e-01,   9.67046769e-01,
        9.67046769e-01,   7.36045180e-01,   4.14397981e-01,
        1.59903635e-01,   3.26064346e-02,  -1.38777878e-17])

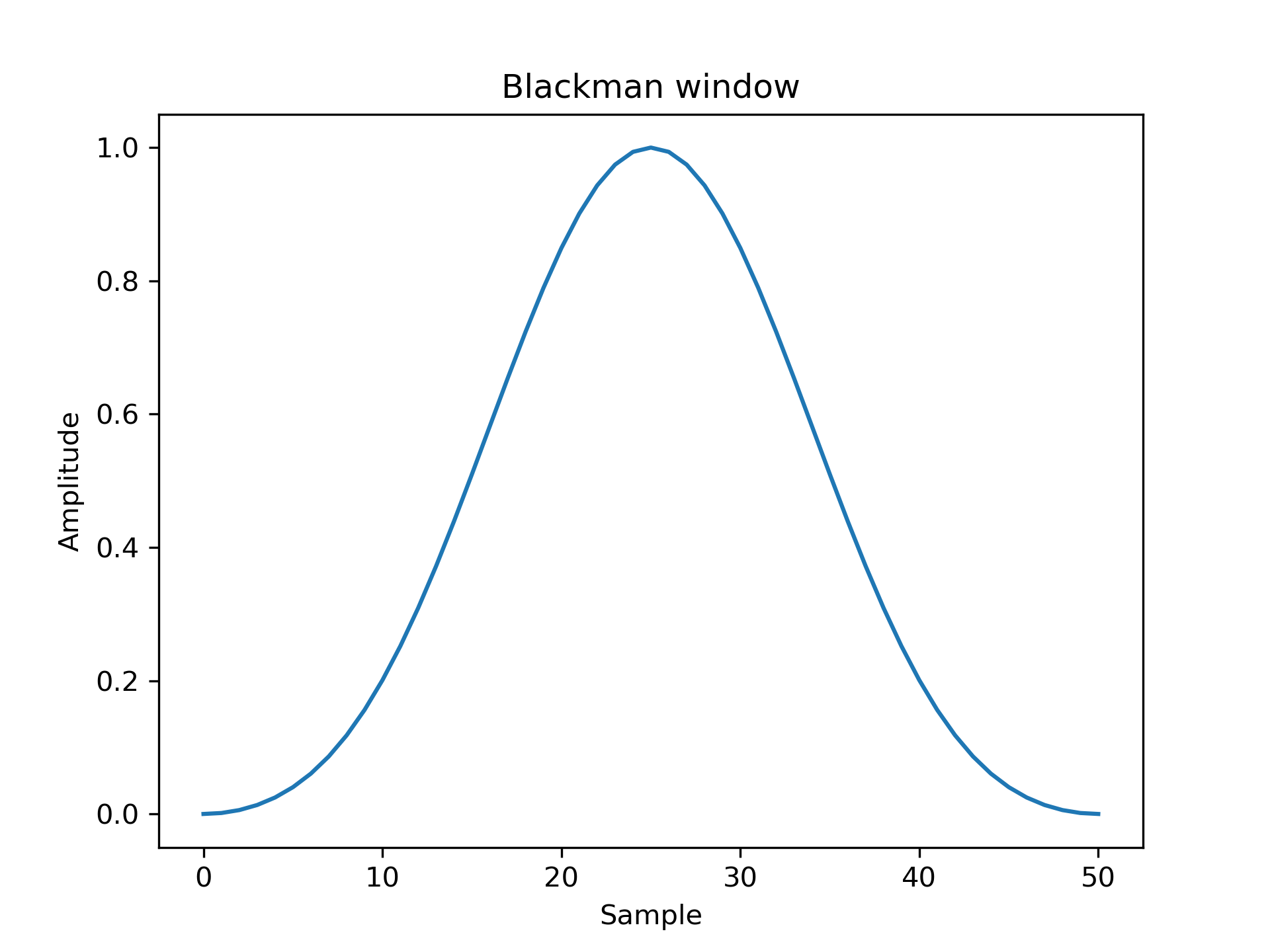
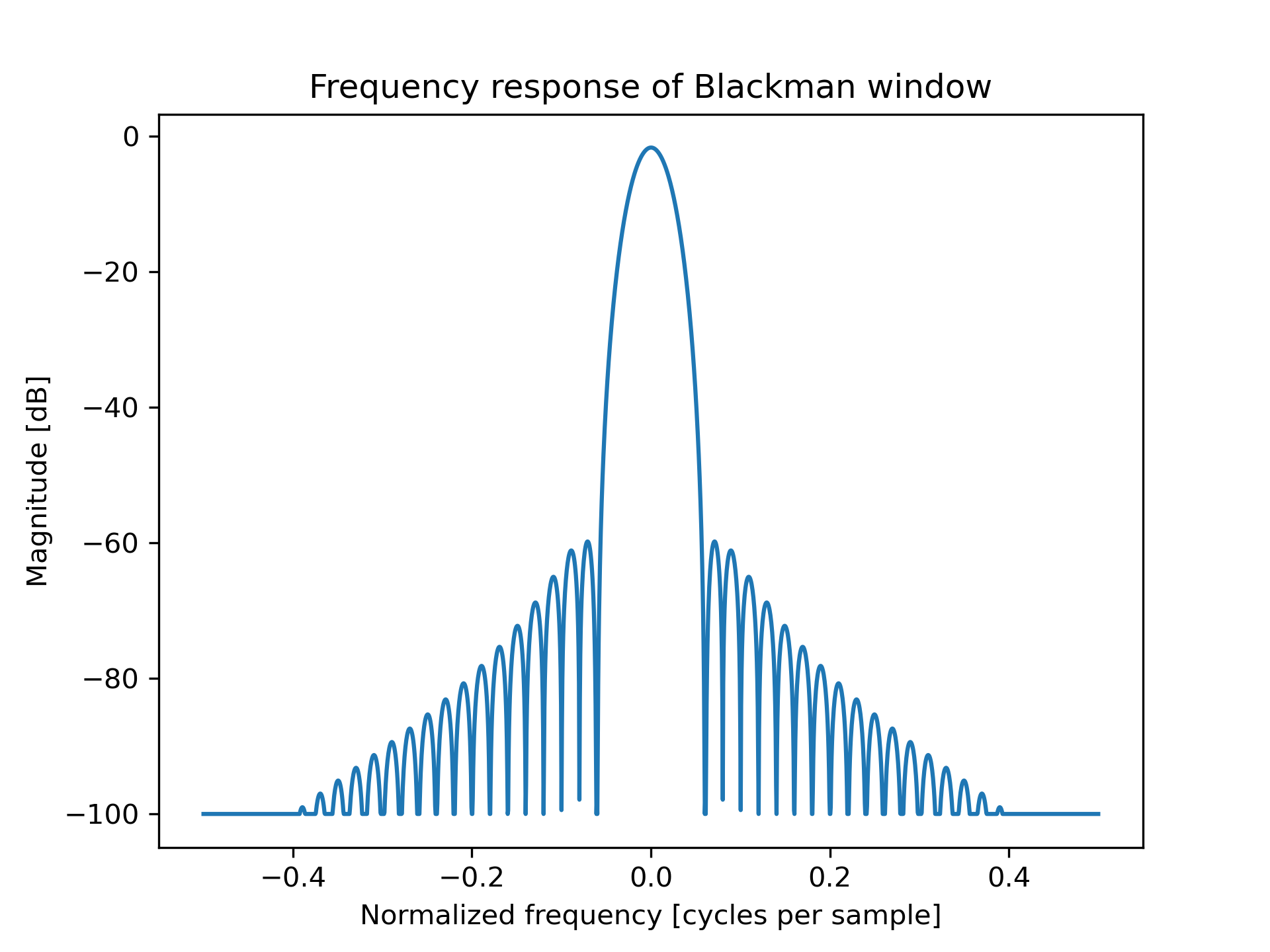
Plot the window and the frequency response:

>>> from numpy.fft import fft, fftshift
... window = np.blackman(51)
... plt.plot(window)
[<matplotlib.lines.Line2D object at 0x...>]

>>> plt.title("Blackman window")
Text(0.5, 1.0, 'Blackman window')

>>> plt.ylabel("Amplitude")
Text(0, 0.5, 'Amplitude')

>>> plt.xlabel("Sample")
Text(0.5, 0, 'Sample')

>>> plt.show()

>>> plt.figure()
<Figure size 640x480 with 0 Axes>

>>> A = fft(window, 2048) / 25.5
... mag = np.abs(fftshift(A))
... freq = np.linspace(-0.5, 0.5, len(A))
... with np.errstate(divide='ignore', invalid='ignore'):
...     response = 20 * np.log10(mag)
...

>>> response = np.clip(response, -100, 100)
... plt.plot(freq, response)
[<matplotlib.lines.Line2D object at 0x...>]

>>> plt.title("Frequency response of Blackman window")
Text(0.5, 1.0, 'Frequency response of Blackman window')

>>> plt.ylabel("Magnitude [dB]")
Text(0, 0.5, 'Magnitude [dB]')

>>> plt.xlabel("Normalized frequency [cycles per sample]")
Text(0.5, 0, 'Normalized frequency [cycles per sample]')

>>> _ = plt.axis('tight')
... plt.show()

See :

Back References

The following pages refer to to this document either explicitly or contain code examples using this.

matplotlib.axes._axes.Axes.cohere matplotlib.pyplot.psd numpy.kaiser matplotlib.pyplot.angle_spectrum matplotlib.axes._axes.Axes.magnitude_spectrum numpy.bartlett matplotlib.pyplot.cohere numpy.hanning matplotlib.mlab.cohere matplotlib.mlab.specgram matplotlib.pyplot.magnitude_spectrum matplotlib.axes._axes.Axes.psd matplotlib.pyplot.phase_spectrum matplotlib.pyplot.csd matplotlib.axes._axes.Axes.csd numpy.hamming matplotlib.mlab.csd matplotlib.axes._axes.Axes.angle_spectrum matplotlib.axes._axes.Axes.phase_spectrum matplotlib.pyplot.specgram matplotlib.axes._axes.Axes.specgram matplotlib.mlab.psd

Local connectivity graph

Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.

Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)

SVG is more flexible but power hungry; and does not scale well to 50 + nodes.

All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them