polyfit(x, y, deg, rcond=None, full=False, w=None, cov=False)
This forms part of the old polynomial API. Since version 1.4, the new polynomial API defined in :None:None:`numpy.polynomial` is preferred. A summary of the differences can be found in the :None:doc:`transition guide </reference/routines.polynomials>`.
Fit a polynomial p(x) = p[0] * x**deg + ... + p[deg]
of degree :None:None:`deg` to points :None:None:`(x, y)`. Returns a vector of coefficients p that minimises the squared error in the order :None:None:`deg`, :None:None:`deg-1`, ... :None:None:`0`.
The :None:None:`Polynomial.fit <numpy.polynomial.polynomial.Polynomial.fit>` class method is recommended for new code as it is more stable numerically. See the documentation of the method for more information.
The solution minimizes the squared error
$$E = \sum_{j=0}^k |p(x_j) - y_j|^2$$in the equations:
x[0]**n * p[0] + ... + x[0] * p[n-1] + p[n] = y[0] x[1]**n * p[0] + ... + x[1] * p[n-1] + p[n] = y[1] ... x[k]**n * p[0] + ... + x[k] * p[n-1] + p[n] = y[k]
The coefficient matrix of the coefficients p is a Vandermonde matrix.
polyfit
issues a RankWarning
when the least-squares fit is badly conditioned. This implies that the best fit is not well-defined due to numerical error. The results may be improved by lowering the polynomial degree or by replacing x by x - x.mean(). The :None:None:`rcond` parameter can also be set to a value smaller than its default, but the resulting fit may be spurious: including contributions from the small singular values can add numerical noise to the result.
Note that fitting polynomial coefficients is inherently badly conditioned when the degree of the polynomial is large or the interval of sample points is badly centered. The quality of the fit should always be checked in these cases. When polynomial fits are not satisfactory, splines may be a good alternative.
x-coordinates of the M sample points (x[i], y[i])
.
y-coordinates of the sample points. Several data sets of sample points sharing the same x-coordinates can be fitted at once by passing in a 2D-array that contains one dataset per column.
Degree of the fitting polynomial
Relative condition number of the fit. Singular values smaller than this relative to the largest singular value will be ignored. The default value is len(x)*eps, where eps is the relative precision of the float type, about 2e-16 in most cases.
Switch determining nature of return value. When it is False (the default) just the coefficients are returned, when True diagnostic information from the singular value decomposition is also returned.
Weights. If not None, the weight w[i]
applies to the unsquared residual y[i] - y_hat[i]
at x[i]
. Ideally the weights are chosen so that the errors of the products w[i]*y[i]
all have the same variance. When using inverse-variance weighting, use w[i] = 1/sigma(y[i])
. The default value is None.
If given and not :None:None:`False`, return not just the estimate but also its covariance matrix. By default, the covariance are scaled by chi2/dof, where dof = M - (deg + 1), i.e., the weights are presumed to be unreliable except in a relative sense and everything is scaled such that the reduced chi2 is unity. This scaling is omitted if cov='unscaled'
, as is relevant for the case that the weights are w = 1/sigma, with sigma known to be a reliable estimate of the uncertainty.
Polynomial coefficients, highest power first. If y was 2-D, the coefficients for :None:None:`k`-th data set are in p[:,k]
.
These values are only returned if full == True
residuals -- sum of squared residuals of the least squares fit
rank -- the effective rank of the scaled Vandermonde
coefficient matrix
singular_values -- singular values of the scaled Vandermonde
coefficient matrix
rcond -- value of :None:None:`rcond`.
For more details, see numpy.linalg.lstsq
.
Present only if full == False
and cov == True
. The covariance matrix of the polynomial coefficient estimates. The diagonal of this matrix are the variance estimates for each coefficient. If y is a 2-D array, then the covariance matrix for the :None:None:`k`-th data set are in V[:,:,k]
Least squares polynomial fit.
The rank of the coefficient matrix in the least-squares fit is deficient. The warning is only raised if full == False
.
The warnings can be turned off by
>>> import warnings
>>> warnings.simplefilter('ignore', np.RankWarning)
linalg.lstsq
Computes a least-squares fit.
polyval
Compute polynomial values.
scipy.interpolate.UnivariateSpline
Computes spline fits.
>>> import warnings
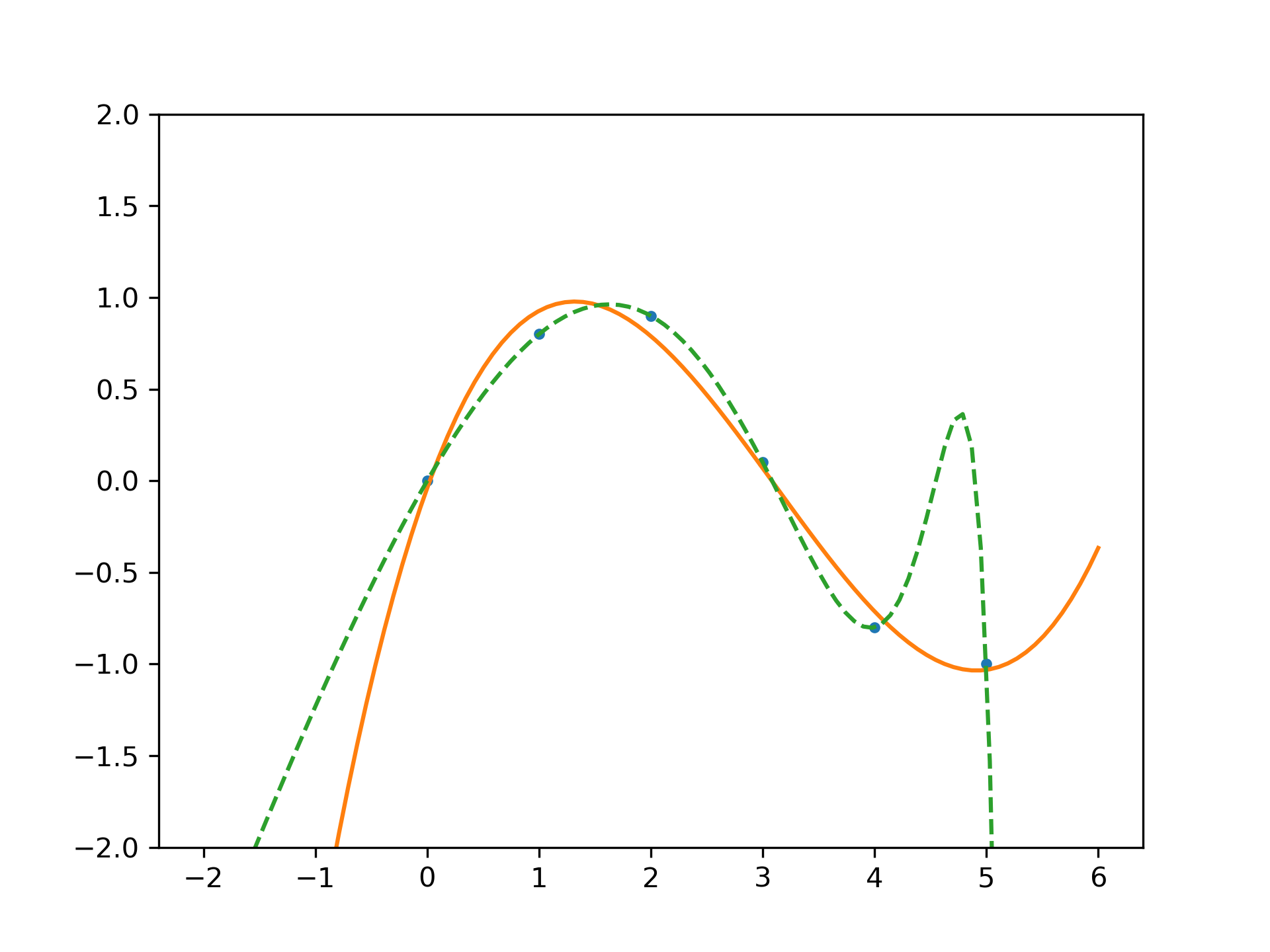
... x = np.array([0.0, 1.0, 2.0, 3.0, 4.0, 5.0])
... y = np.array([0.0, 0.8, 0.9, 0.1, -0.8, -1.0])
... z = np.polyfit(x, y, 3)
... z array([ 0.08703704, -0.81349206, 1.69312169, -0.03968254]) # may vary
It is convenient to use poly1d
objects for dealing with polynomials:
>>> p = np.poly1d(z)
... p(0.5) 0.6143849206349179 # may vary
>>> p(3.5) -0.34732142857143039 # may vary
>>> p(10) 22.579365079365115 # may vary
High-order polynomials may oscillate wildly:
>>> with warnings.catch_warnings():
... warnings.simplefilter('ignore', np.RankWarning)
... p30 = np.poly1d(np.polyfit(x, y, 30)) ...
>>> p30(4) -0.80000000000000204 # may vary
>>> p30(5) -0.99999999999999445 # may vary
>>> p30(4.5) -0.10547061179440398 # may vary
Illustration:
>>> import matplotlib.pyplot as plt
... xp = np.linspace(-2, 6, 100)
... _ = plt.plot(x, y, '.', xp, p(xp), '-', xp, p30(xp), '--')
... plt.ylim(-2,2) (-2, 2)
>>> plt.show()
The following pages refer to to this document either explicitly or contain code examples using this.
numpy.RankWarning
numpy.roots
numpy.polynomial.polynomial.polyfit
numpy.ma.extras.polyfit
numpy.poly
numpy.polyfit
numpy.polymul
papyri
numpy.polydiv
numpy.polyadd
Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.
Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)
SVG is more flexible but power hungry; and does not scale well to 50 + nodes.
All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them