Fits a spline y = spl(x) of degree k to the provided x, y data. s specifies the number of knots by specifying a smoothing condition.
The number of data points must be larger than the spline degree k.
NaN handling: If the input arrays contain nan
values, the result is not useful, since the underlying spline fitting routines cannot deal with nan
. A workaround is to use zero weights for not-a-number data points:
>>> from scipy.interpolate import UnivariateSpline >>> x, y = np.array([1, 2, 3, 4]), np.array([1, np.nan, 3, 4]) >>> w = np.isnan(y) >>> y[w] = 0. >>> spl = UnivariateSpline(x, y, w=~w)
Notice the need to replace a nan
by a numerical value (precise value does not matter as long as the corresponding weight is zero.)
1-D array of independent input data. Must be increasing; must be strictly increasing if s is 0.
1-D array of dependent input data, of the same length as x.
Weights for spline fitting. Must be positive. If w is None, weights are all equal. Default is None.
2-sequence specifying the boundary of the approximation interval. If :None:None:`bbox` is None, bbox=[x[0], x[-1]]
. Default is None.
Degree of the smoothing spline. Must be 1 <= k <= 5. k = 3
is a cubic spline. Default is 3.
Positive smoothing factor used to choose the number of knots. Number of knots will be increased until the smoothing condition is satisfied:
sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) <= s
If s is None, s = len(w)
which should be a good value if 1/w[i]
is an estimate of the standard deviation of y[i]
. If 0, spline will interpolate through all data points. Default is None.
Controls the extrapolation mode for elements not in the interval defined by the knot sequence.
if ext=0 or 'extrapolate', return the extrapolated value.
if ext=1 or 'zeros', return 0
if ext=2 or 'raise', raise a ValueError
if ext=3 of 'const', return the boundary value.
Default is 0.
Whether to check that the input arrays contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination or non-sensical results) if the inputs do contain infinities or NaNs. Default is False.
1-D smoothing spline fit to a given set of data points.
BivariateSpline
a base class for bivariate splines.
InterpolatedUnivariateSpline
a interpolating univariate spline for a given set of data points.
LSQBivariateSpline
a bivariate spline using weighted least-squares fitting
LSQSphereBivariateSpline
a bivariate spline in spherical coordinates using weighted least-squares fitting
RectBivariateSpline
a bivariate spline over a rectangular mesh
RectSphereBivariateSpline
a bivariate spline over a rectangular mesh on a sphere
SmoothBivariateSpline
a smoothing bivariate spline through the given points
SmoothSphereBivariateSpline
a smoothing bivariate spline in spherical coordinates
bisplev
a function to evaluate a bivariate B-spline and its derivatives
bisplrep
a function to find a bivariate B-spline representation of a surface
spalde
a function to evaluate all derivatives of a B-spline
splev
a function to evaluate a B-spline or its derivatives
splint
a function to evaluate the definite integral of a B-spline between two given points
splrep
a function to find the B-spline representation of a 1-D curve
sproot
a function to find the roots of a cubic B-spline
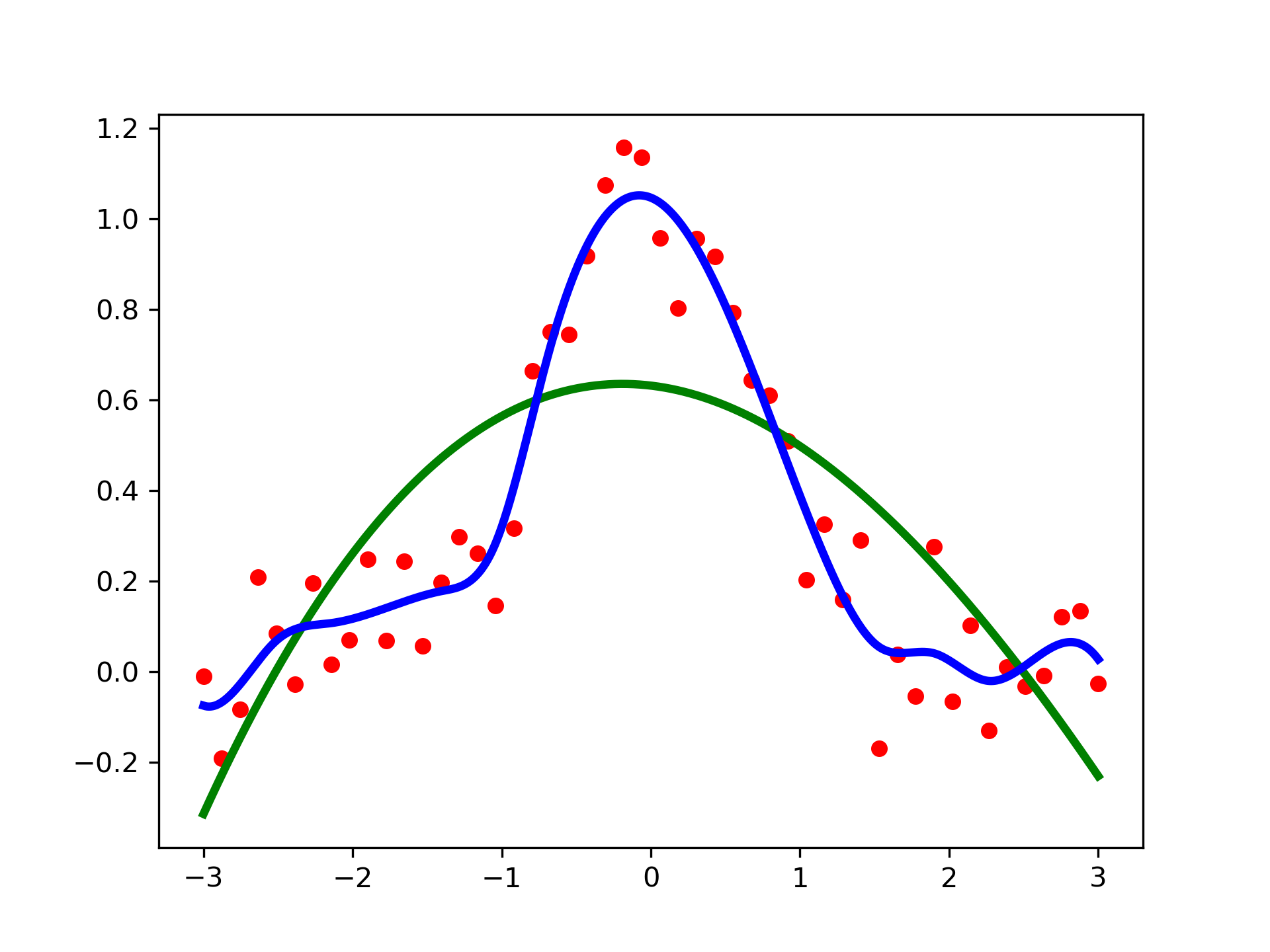
>>> import matplotlib.pyplot as plt
... from scipy.interpolate import UnivariateSpline
... rng = np.random.default_rng()
... x = np.linspace(-3, 3, 50)
... y = np.exp(-x**2) + 0.1 * rng.standard_normal(50)
... plt.plot(x, y, 'ro', ms=5)
Use the default value for the smoothing parameter:
>>> spl = UnivariateSpline(x, y)
... xs = np.linspace(-3, 3, 1000)
... plt.plot(xs, spl(xs), 'g', lw=3)
Manually change the amount of smoothing:
>>> spl.set_smoothing_factor(0.5)
... plt.plot(xs, spl(xs), 'b', lw=3)
... plt.show()
The following pages refer to to this document either explicitly or contain code examples using this.
scipy.interpolate._fitpack2.UnivariateSpline.integral
scipy.interpolate._fitpack2.UnivariateSpline.derivatives
scipy.interpolate._fitpack2.BivariateSpline
scipy.interpolate._fitpack2.RectBivariateSpline
scipy.interpolate._fitpack2.SphereBivariateSpline
scipy.interpolate._fitpack2.SmoothBivariateSpline
scipy.interpolate._fitpack2.UnivariateSpline.derivative
scipy.interpolate._fitpack_impl.splint
scipy.interpolate._fitpack2.UnivariateSpline.antiderivative
scipy.interpolate._fitpack_impl.sproot
scipy.interpolate._fitpack2.LSQUnivariateSpline
scipy.interpolate._fitpack2.UnivariateSpline
scipy.interpolate._fitpack2.RectSphereBivariateSpline
papyri.examples.example2
scipy.interpolate._fitpack_impl.splrep
scipy.special._ellip_harm.ellip_harm
scipy.interpolate._fitpack2.LSQSphereBivariateSpline
papyri
scipy.interpolate._fitpack2.LSQBivariateSpline
scipy.interpolate._fitpack2.SmoothSphereBivariateSpline
scipy.interpolate._fitpack_impl.splprep
scipy.interpolate._fitpack_impl.bisplrep
scipy.interpolate._fitpack_py.splrep
scipy.interpolate._fitpack2.InterpolatedUnivariateSpline
scipy.interpolate._interpolate.interp1d
scipy.interpolate._bsplines.make_interp_spline
Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.
Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)
SVG is more flexible but power hungry; and does not scale well to 50 + nodes.
All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them