make_interp_spline(x, y, k=3, t=None, bc_type=None, axis=0, check_finite=True)

Parameters

x : array_like, shape (n,)

Abscissas.

y : array_like, shape (n, ...)

Ordinates.

k : int, optional

B-spline degree. Default is cubic, k=3.

t : array_like, shape (nt + k + 1,), optional.

Knots. The number of knots needs to agree with the number of datapoints and the number of derivatives at the edges. Specifically, nt - n must equal len(deriv_l) + len(deriv_r) .

bc_type : 2-tuple or None

Boundary conditions. Default is None, which means choosing the boundary conditions automatically. Otherwise, it must be a length-two tuple where the first element sets the boundary conditions at x[0] and the second element sets the boundary conditions at x[-1] . Each of these must be an iterable of pairs (order, value) which gives the values of derivatives of specified orders at the given edge of the interpolation interval. Alternatively, the following string aliases are recognized:

• "clamped" : The first derivatives at the ends are zero. This is

  equivalent to bc_type=([(1, 0.0)], [(1, 0.0)]) .

• "natural" : The second derivatives at ends are zero. This is equivalent to bc_type=([(2, 0.0)], [(2, 0.0)]) .

• "not-a-knot" (default): The first and second segments are the same polynomial. This is equivalent to having bc_type=None .

• "periodic" : The values and the first k-1 derivatives at the ends are equivalent.

axis : int, optional

Interpolation axis. Default is 0.

check_finite : bool, optional

Whether to check that the input arrays contain only finite numbers. Disabling may give a performance gain, but may result in problems (crashes, non-termination) if the inputs do contain infinities or NaNs. Default is True.

Returns

b : a BSpline object of the degree ``k`` and with knots ``t``.

Compute the (coefficients of) interpolating B-spline.

See Also

BSpline

base class representing the B-spline objects

CubicSpline

a cubic spline in the polynomial basis

UnivariateSpline

a wrapper over FITPACK spline fitting routines

make_lsq_spline

a similar factory function for spline fitting

splrep

a wrapper over FITPACK spline fitting routines

Examples

Use cubic interpolation on Chebyshev nodes:

>>> def cheb_nodes(N):
...     jj = 2.*np.arange(N) + 1
...     x = np.cos(np.pi * jj / 2 / N)[::-1]
...     return x

>>> x = cheb_nodes(20)
... y = np.sqrt(1 - x**2)

>>> from scipy.interpolate import BSpline, make_interp_spline
... b = make_interp_spline(x, y)
... np.allclose(b(x), y)
True

Note that the default is a cubic spline with a not-a-knot boundary condition

>>> b.k
3

Here we use a 'natural' spline, with zero 2nd derivatives at edges:

>>> l, r = [(2, 0.0)], [(2, 0.0)]
... b_n = make_interp_spline(x, y, bc_type=(l, r))  # or, bc_type="natural"
... np.allclose(b_n(x), y)
True

>>> x0, x1 = x[0], x[-1]
... np.allclose([b_n(x0, 2), b_n(x1, 2)], [0, 0])
True

Interpolation of parametric curves is also supported. As an example, we compute a discretization of a snail curve in polar coordinates

>>> phi = np.linspace(0, 2.*np.pi, 40)
... r = 0.3 + np.cos(phi)
... x, y = r*np.cos(phi), r*np.sin(phi)  # convert to Cartesian coordinates

Build an interpolating curve, parameterizing it by the angle

>>> from scipy.interpolate import make_interp_spline
... spl = make_interp_spline(phi, np.c_[x, y])

Evaluate the interpolant on a finer grid (note that we transpose the result to unpack it into a pair of x- and y-arrays)

>>> phi_new = np.linspace(0, 2.*np.pi, 100)
... x_new, y_new = spl(phi_new).T

Plot the result

>>> import matplotlib.pyplot as plt
... plt.plot(x, y, 'o')
... plt.plot(x_new, y_new, '-')
... plt.show()

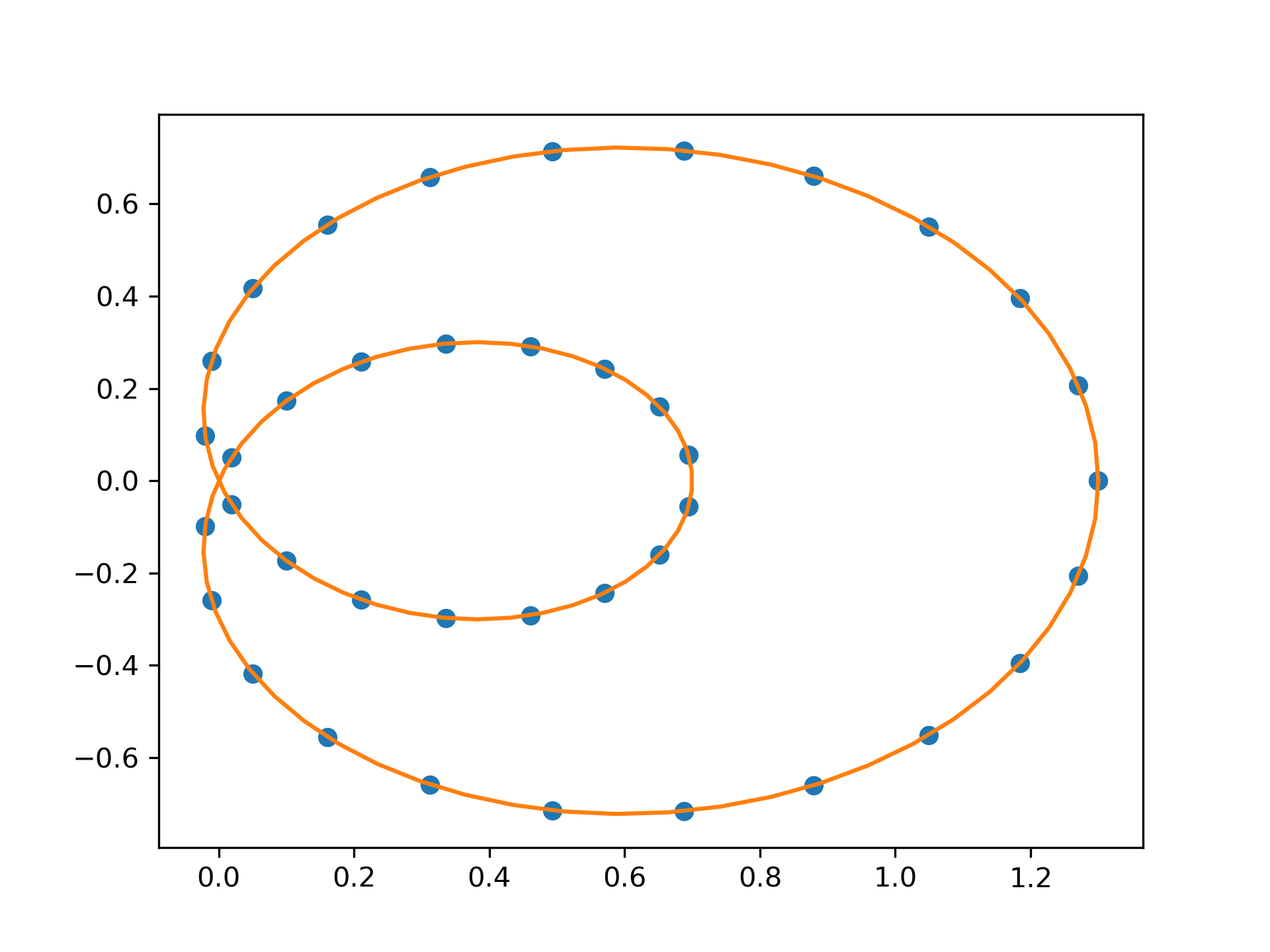
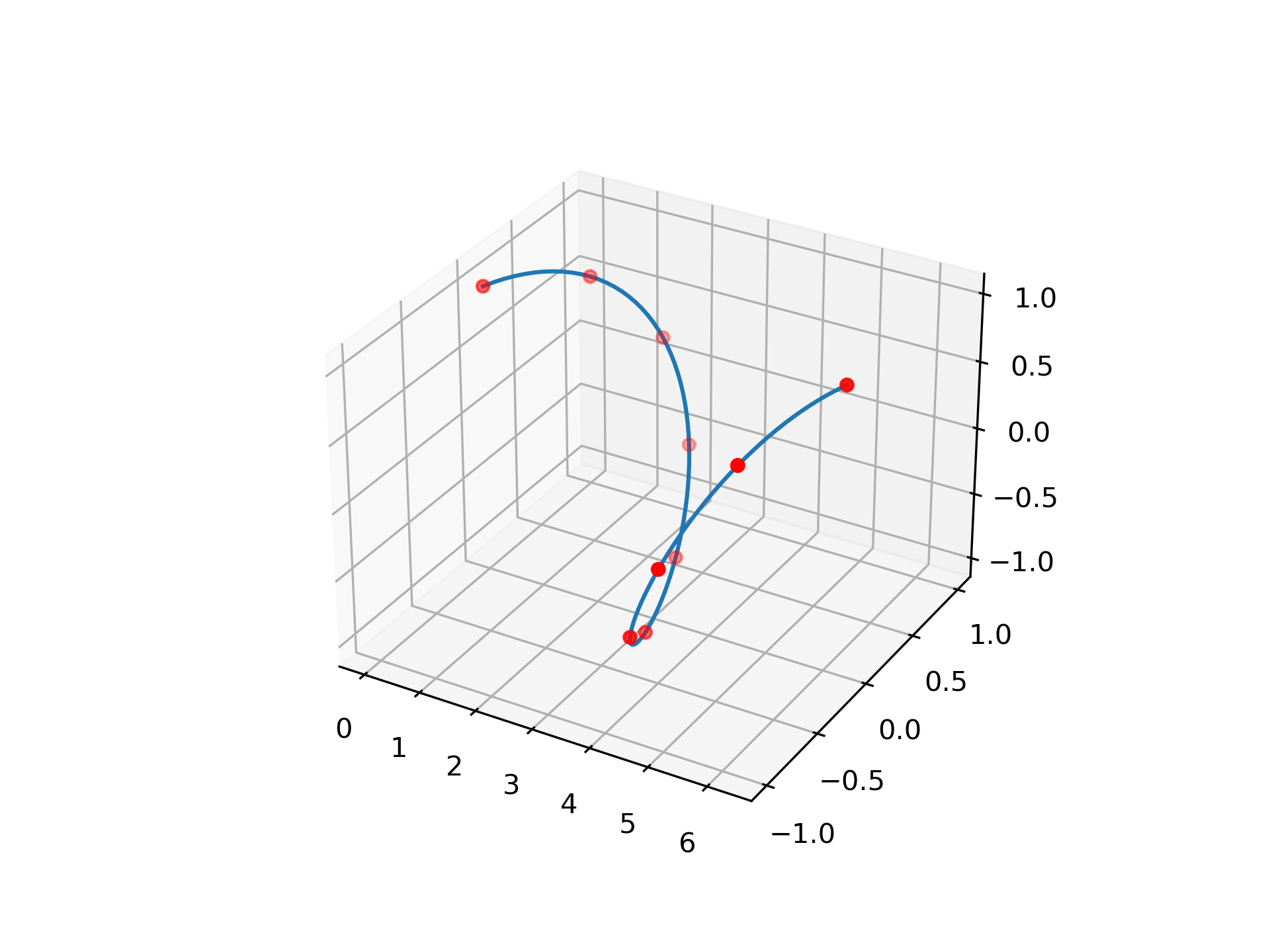
Build a B-spline curve with 2 dimensional y

>>> x = np.linspace(0, 2*np.pi, 10)
... y = np.array([np.sin(x), np.cos(x)])

Periodic condition is satisfied because y coordinates of points on the ends are equivalent

>>> ax = plt.axes(projection='3d')
... xx = np.linspace(0, 2*np.pi, 100)
... bspl = make_interp_spline(x, y, k=5, bc_type='periodic', axis=1)
... ax.plot3D(xx, *bspl(xx))
... ax.scatter3D(x, *y, color='red')
... plt.show()

See :

Back References

The following pages refer to to this document either explicitly or contain code examples using this.

scipy.interpolate._fitpack_py.splrep scipy.interpolate._bsplines.make_lsq_spline scipy.interpolate._bsplines.make_interp_spline

Local connectivity graph

Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.

Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)

SVG is more flexible but power hungry; and does not scale well to 50 + nodes.

All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them

---

GitHub : /scipy/interpolate/_bsplines.py#1093
type: <class 'function'>
Commit: