periodogram(x, fs=1.0, window='boxcar', nfft=None, detrend='constant', return_onesided=True, scaling='density', axis=-1)
Time series of measurement values
Sampling frequency of the x time series. Defaults to 1.0.
Desired window to use. If :None:None:`window` is a string or tuple, it is passed to get_window
to generate the window values, which are DFT-even by default. See get_window
for a list of windows and required parameters. If :None:None:`window` is array_like it will be used directly as the window and its length must be nperseg. Defaults to 'boxcar'.
Length of the FFT used. If :None:None:`None` the length of x will be used.
Specifies how to detrend each segment. If detrend
is a string, it is passed as the :None:None:`type` argument to the detrend
function. If it is a function, it takes a segment and returns a detrended segment. If detrend
is :None:None:`False`, no detrending is done. Defaults to 'constant'.
If :None:None:`True`, return a one-sided spectrum for real data. If :None:None:`False` return a two-sided spectrum. Defaults to :None:None:`True`, but for complex data, a two-sided spectrum is always returned.
Selects between computing the power spectral density ('density') where :None:None:`Pxx` has units of V**2/Hz and computing the power spectrum ('spectrum') where :None:None:`Pxx` has units of V**2, if x is measured in V and :None:None:`fs` is measured in Hz. Defaults to 'density'
Axis along which the periodogram is computed; the default is over the last axis (i.e. axis=-1
).
Array of sample frequencies.
Power spectral density or power spectrum of x.
Estimate power spectral density using a periodogram.
lombscargle
Lomb-Scargle periodogram for unevenly sampled data
welch
Estimate power spectral density using Welch's method
>>> from scipy import signal
... import matplotlib.pyplot as plt
... rng = np.random.default_rng()
Generate a test signal, a 2 Vrms sine wave at 1234 Hz, corrupted by 0.001 V**2/Hz of white noise sampled at 10 kHz.
>>> fs = 10e3
... N = 1e5
... amp = 2*np.sqrt(2)
... freq = 1234.0
... noise_power = 0.001 * fs / 2
... time = np.arange(N) / fs
... x = amp*np.sin(2*np.pi*freq*time)
... x += rng.normal(scale=np.sqrt(noise_power), size=time.shape)
Compute and plot the power spectral density.
>>> f, Pxx_den = signal.periodogram(x, fs)
... plt.semilogy(f, Pxx_den)
... plt.ylim([1e-7, 1e2])
... plt.xlabel('frequency [Hz]')
... plt.ylabel('PSD [V**2/Hz]')
... plt.show()
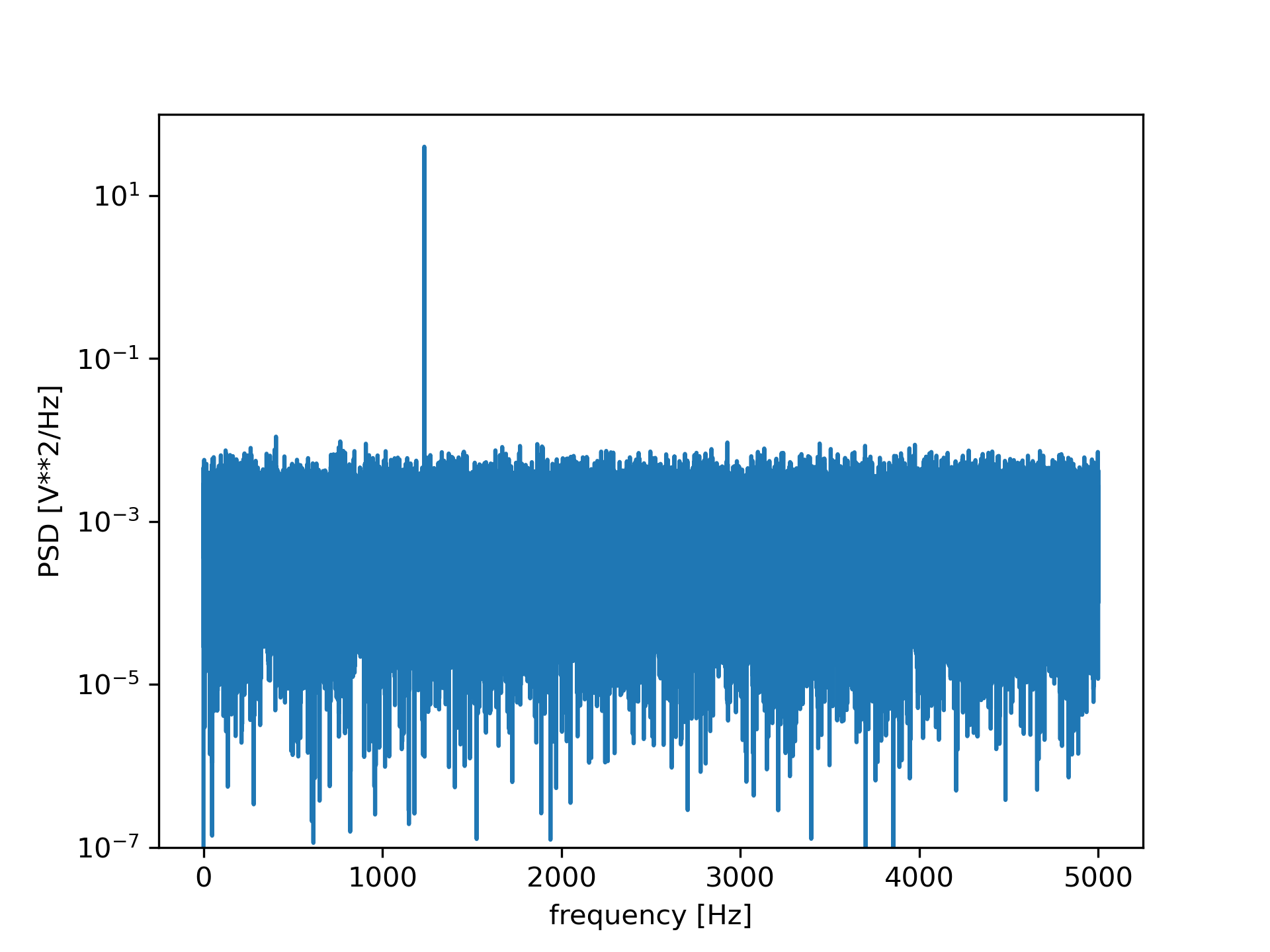
If we average the last half of the spectral density, to exclude the peak, we can recover the noise power on the signal.
>>> np.mean(Pxx_den[25000:]) 0.000985320699252543
Now compute and plot the power spectrum.
>>> f, Pxx_spec = signal.periodogram(x, fs, 'flattop', scaling='spectrum')
... plt.figure()
... plt.semilogy(f, np.sqrt(Pxx_spec))
... plt.ylim([1e-4, 1e1])
... plt.xlabel('frequency [Hz]')
... plt.ylabel('Linear spectrum [V RMS]')
... plt.show()
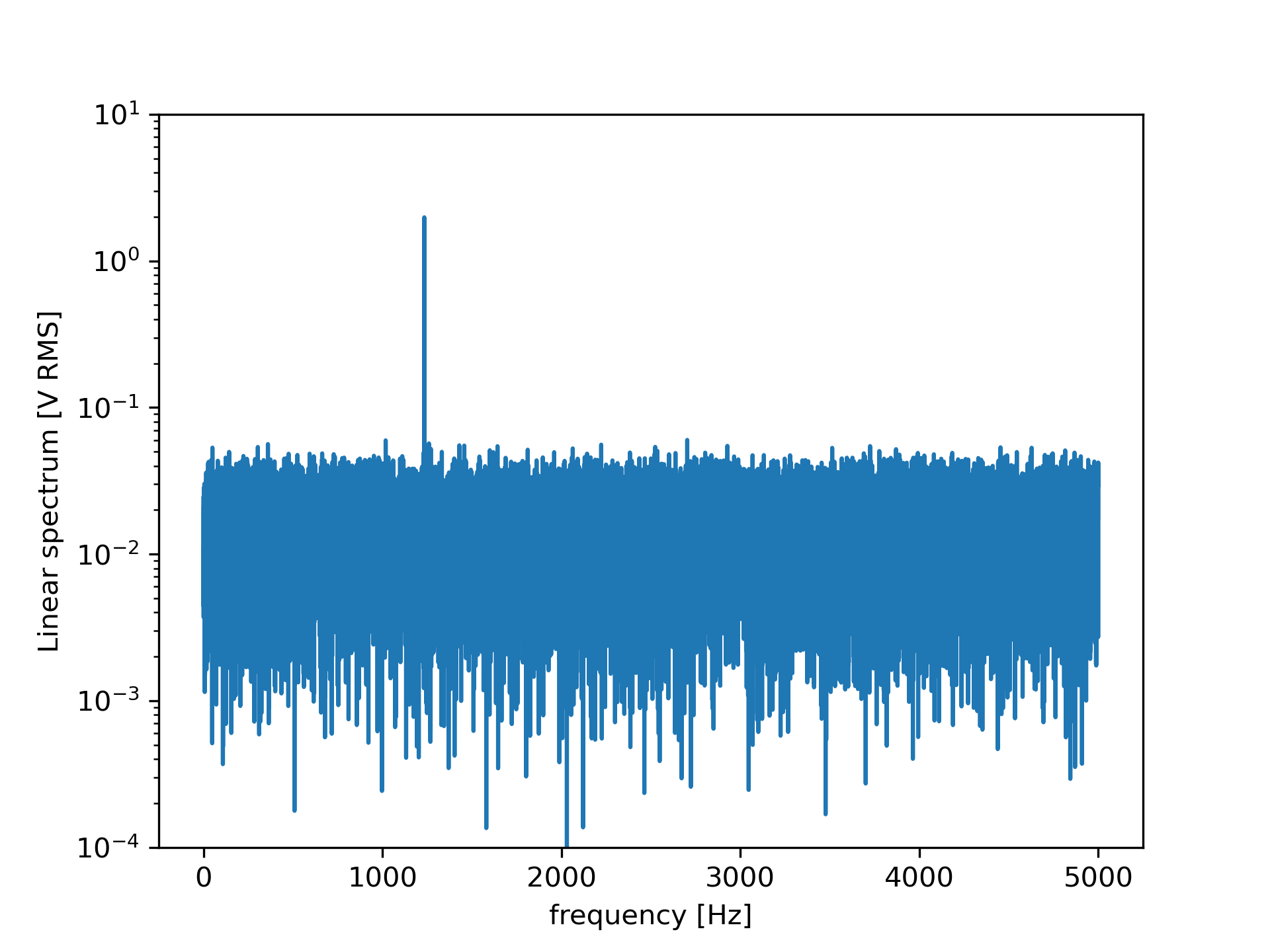
The peak height in the power spectrum is an estimate of the RMS amplitude.
>>> np.sqrt(Pxx_spec.max()) 2.0077340678640727See :
The following pages refer to to this document either explicitly or contain code examples using this.
scipy.signal._spectral_py.welch
scipy.signal._spectral_py.coherence
scipy.signal._spectral_py.csd
scipy.signal._spectral_py.periodogram
scipy.signal._spectral_py.spectrogram
Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.
Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)
SVG is more flexible but power hungry; and does not scale well to 50 + nodes.
All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them