chirp(t, f0, t1, f1, method='linear', phi=0, vertex_zero=True)
In the following, 'Hz' should be interpreted as 'cycles per unit'; there is no requirement here that the unit is one second. The important distinction is that the units of rotation are cycles, not radians. Likewise, t could be a measurement of space instead of time.
There are four options for the method
. The following formulas give the instantaneous frequency (in Hz) of the signal generated by :None:None:`chirp()`. For convenience, the shorter names shown below may also be used.
linear, lin, li:
f(t) = f0 + (f1 - f0) * t / t1
quadratic, quad, q:
The graph of the frequency f(t) is a parabola through (0, f0) and (t1, f1). By default, the vertex of the parabola is at (0, f0). If
:None:None:`vertex_zero`is False, then the vertex is at (t1, f1). The formula is:if vertex_zero is True:
f(t) = f0 + (f1 - f0) * t**2 / t1**2else:
f(t) = f1 - (f1 - f0) * (t1 - t)**2 / t1**2To use a more general quadratic function, or an arbitrary polynomial, use the function
scipy.signal.sweep_poly.
logarithmic, log, lo:
f(t) = f0 * (f1/f0)**(t/t1)f0 and f1 must be nonzero and have the same sign.
This signal is also known as a geometric or exponential chirp.
hyperbolic, hyp:
f(t) = f0*f1*t1 / ((f0 - f1)*t + f1*t1)f0 and f1 must be nonzero.
Times at which to evaluate the waveform.
Frequency (e.g. Hz) at time t=0.
Time at which :None:None:`f1` is specified.
Frequency (e.g. Hz) of the waveform at time :None:None:`t1`.
Kind of frequency sweep. If not given, :None:None:`linear` is assumed. See Notes below for more details.
Phase offset, in degrees. Default is 0.
This parameter is only used when method
is 'quadratic'. It determines whether the vertex of the parabola that is the graph of the frequency is at t=0 or t=t1.
A numpy array containing the signal evaluated at t with the requested time-varying frequency. More precisely, the function returns cos(phase + (pi/180)*phi)
where :None:None:`phase` is the integral (from 0 to t) of 2*pi*f(t)
. f(t)
is defined below.
Frequency-swept cosine generator.
The following will be used in the examples:
>>> from scipy.signal import chirp, spectrogram
... import matplotlib.pyplot as plt
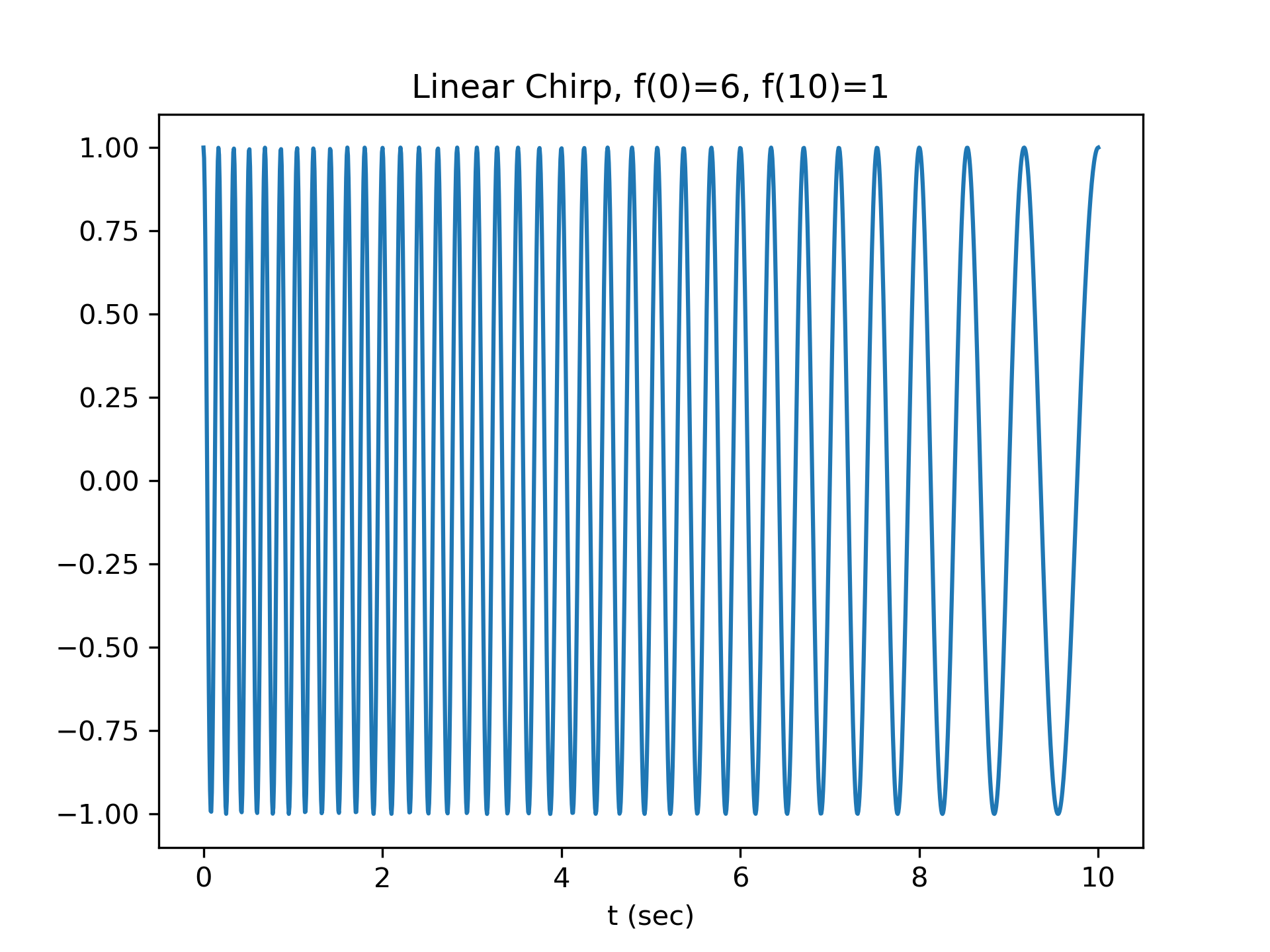
For the first example, we'll plot the waveform for a linear chirp from 6 Hz to 1 Hz over 10 seconds:
>>> t = np.linspace(0, 10, 1500)
... w = chirp(t, f0=6, f1=1, t1=10, method='linear')
... plt.plot(t, w)
... plt.title("Linear Chirp, f(0)=6, f(10)=1")
... plt.xlabel('t (sec)')
... plt.show()
For the remaining examples, we'll use higher frequency ranges, and demonstrate the result using scipy.signal.spectrogram
. We'll use a 4 second interval sampled at 7200 Hz.
>>> fs = 7200
... T = 4
... t = np.arange(0, int(T*fs)) / fs
We'll use this function to plot the spectrogram in each example.
>>> def plot_spectrogram(title, w, fs):
... ff, tt, Sxx = spectrogram(w, fs=fs, nperseg=256, nfft=576)
... plt.pcolormesh(tt, ff[:145], Sxx[:145], cmap='gray_r', shading='gouraud')
... plt.title(title)
... plt.xlabel('t (sec)')
... plt.ylabel('Frequency (Hz)')
... plt.grid() ...
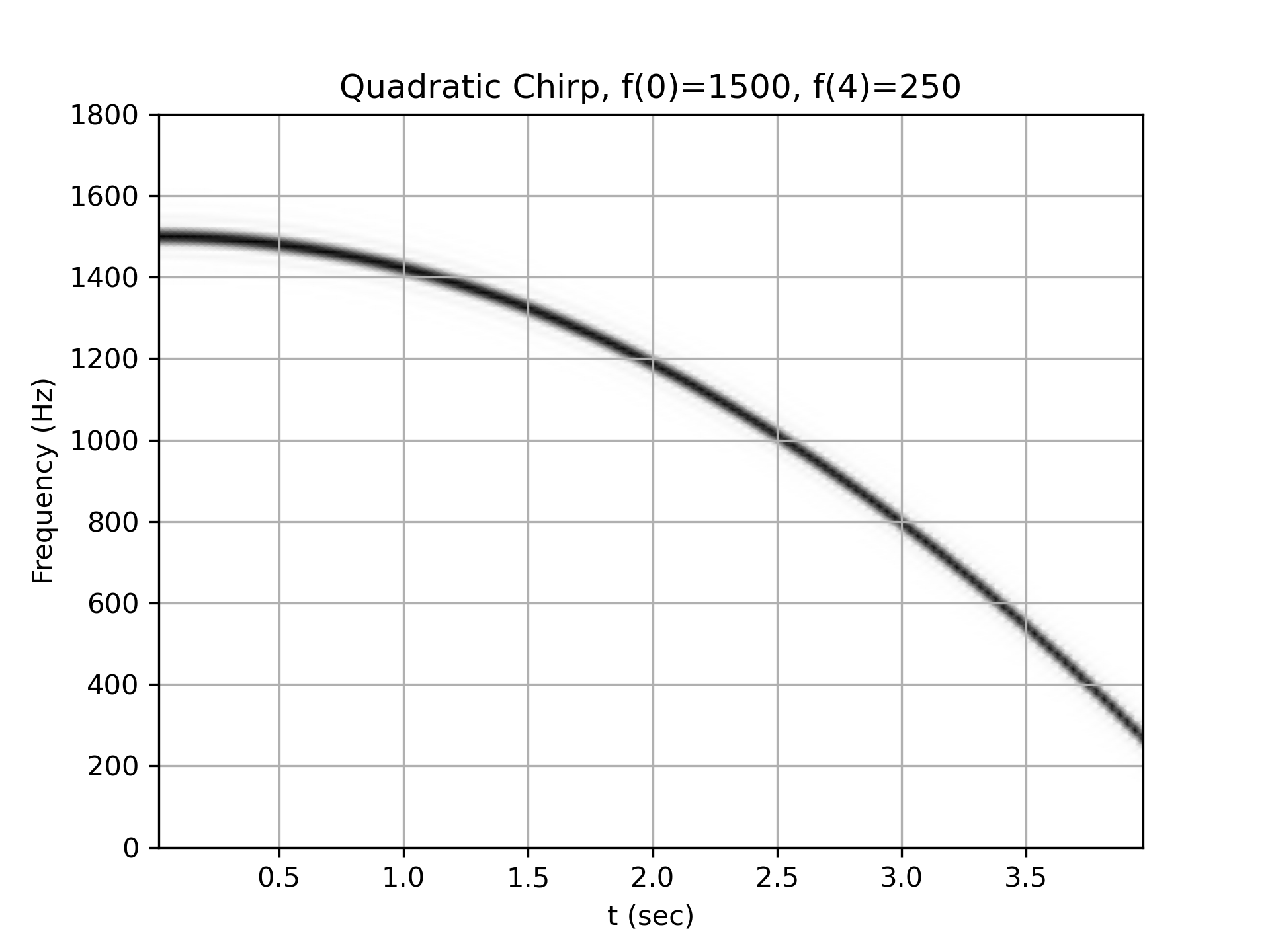
Quadratic chirp from 1500 Hz to 250 Hz (vertex of the parabolic curve of the frequency is at t=0):
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic')
... plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250', w, fs)
... plt.show()
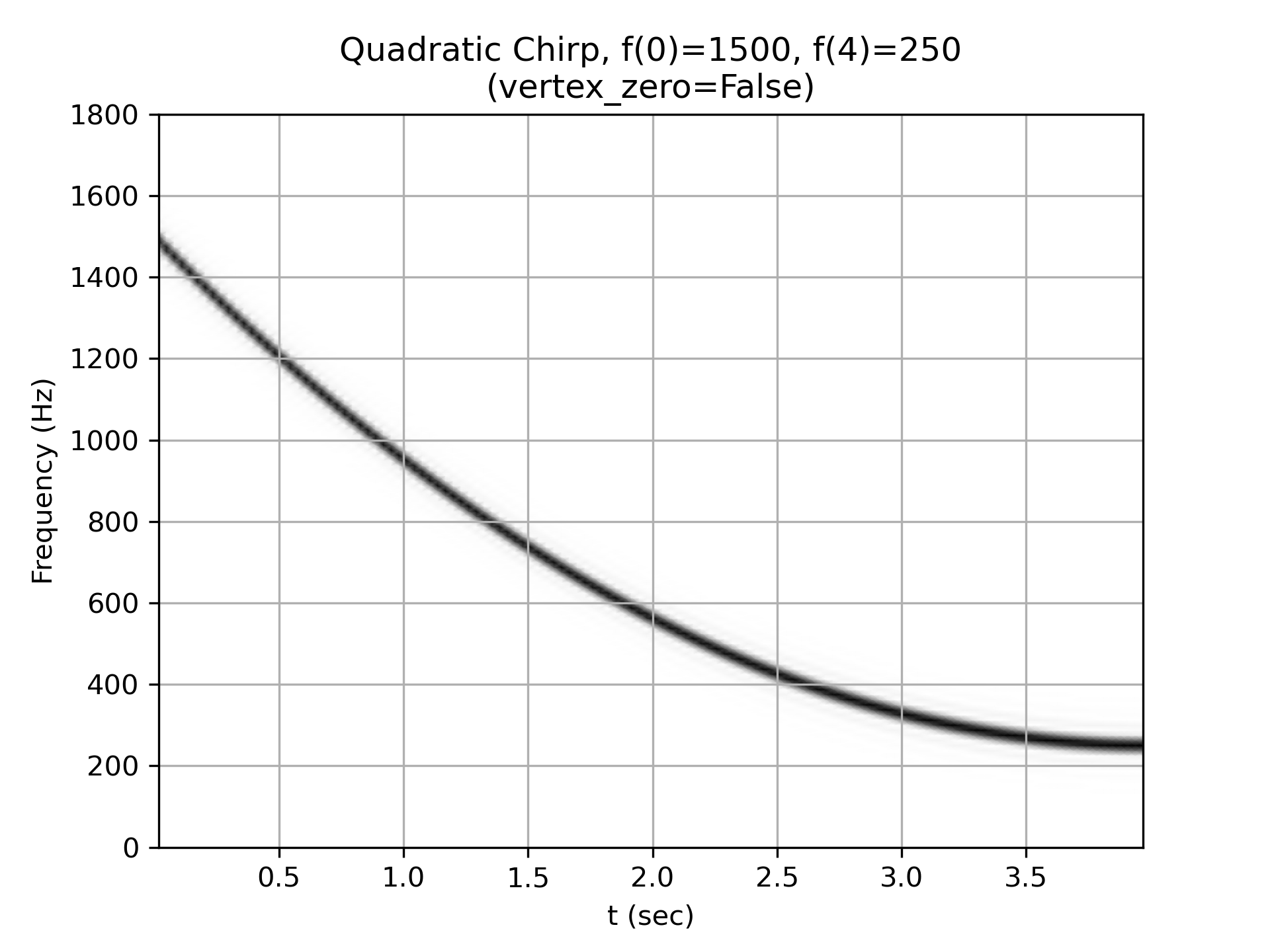
Quadratic chirp from 1500 Hz to 250 Hz (vertex of the parabolic curve of the frequency is at t=T):
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='quadratic',
... vertex_zero=False)
... plot_spectrogram(f'Quadratic Chirp, f(0)=1500, f({T})=250\n' +
... '(vertex_zero=False)', w, fs)
... plt.show()
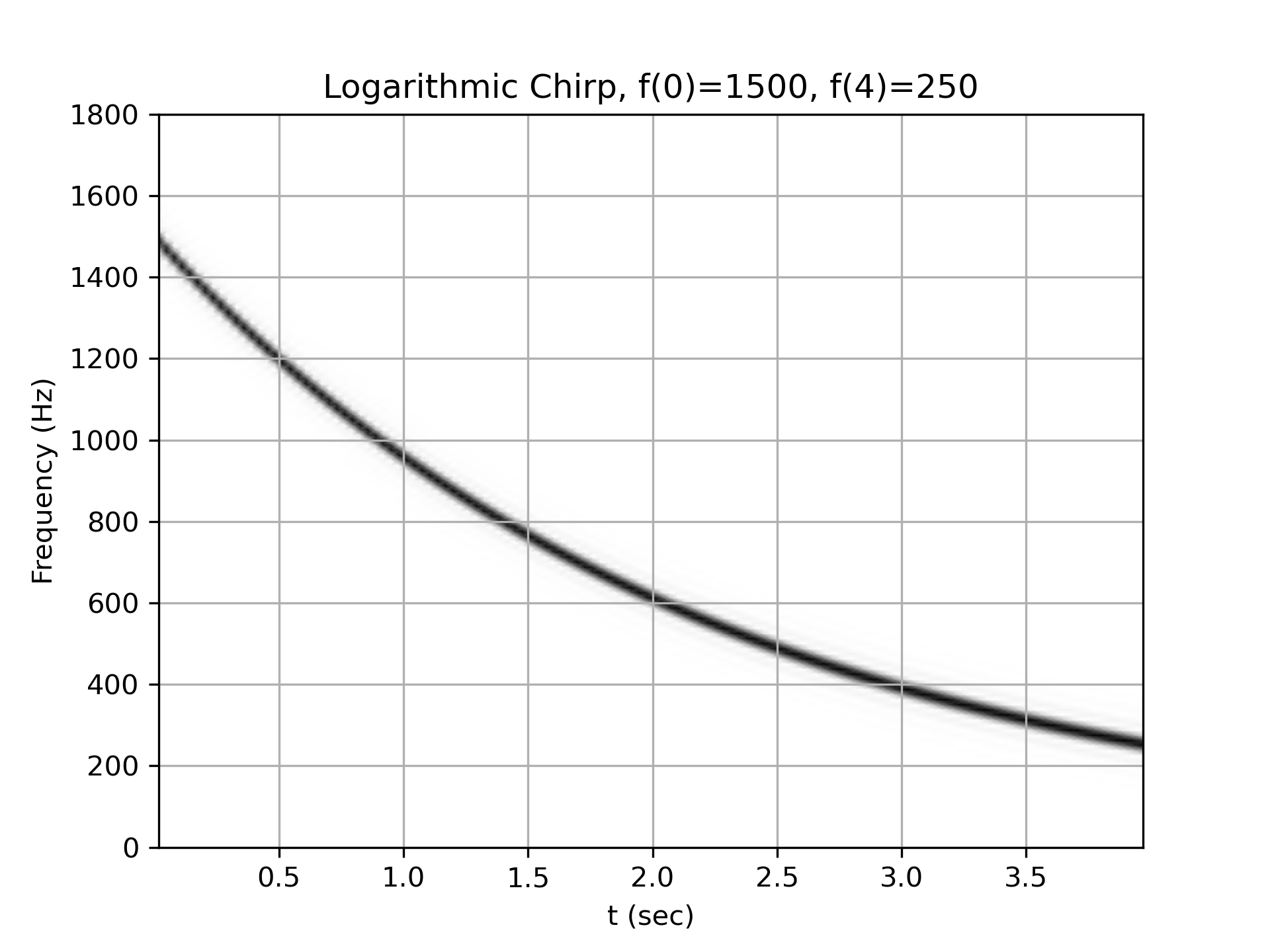
Logarithmic chirp from 1500 Hz to 250 Hz:
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='logarithmic')
... plot_spectrogram(f'Logarithmic Chirp, f(0)=1500, f({T})=250', w, fs)
... plt.show()
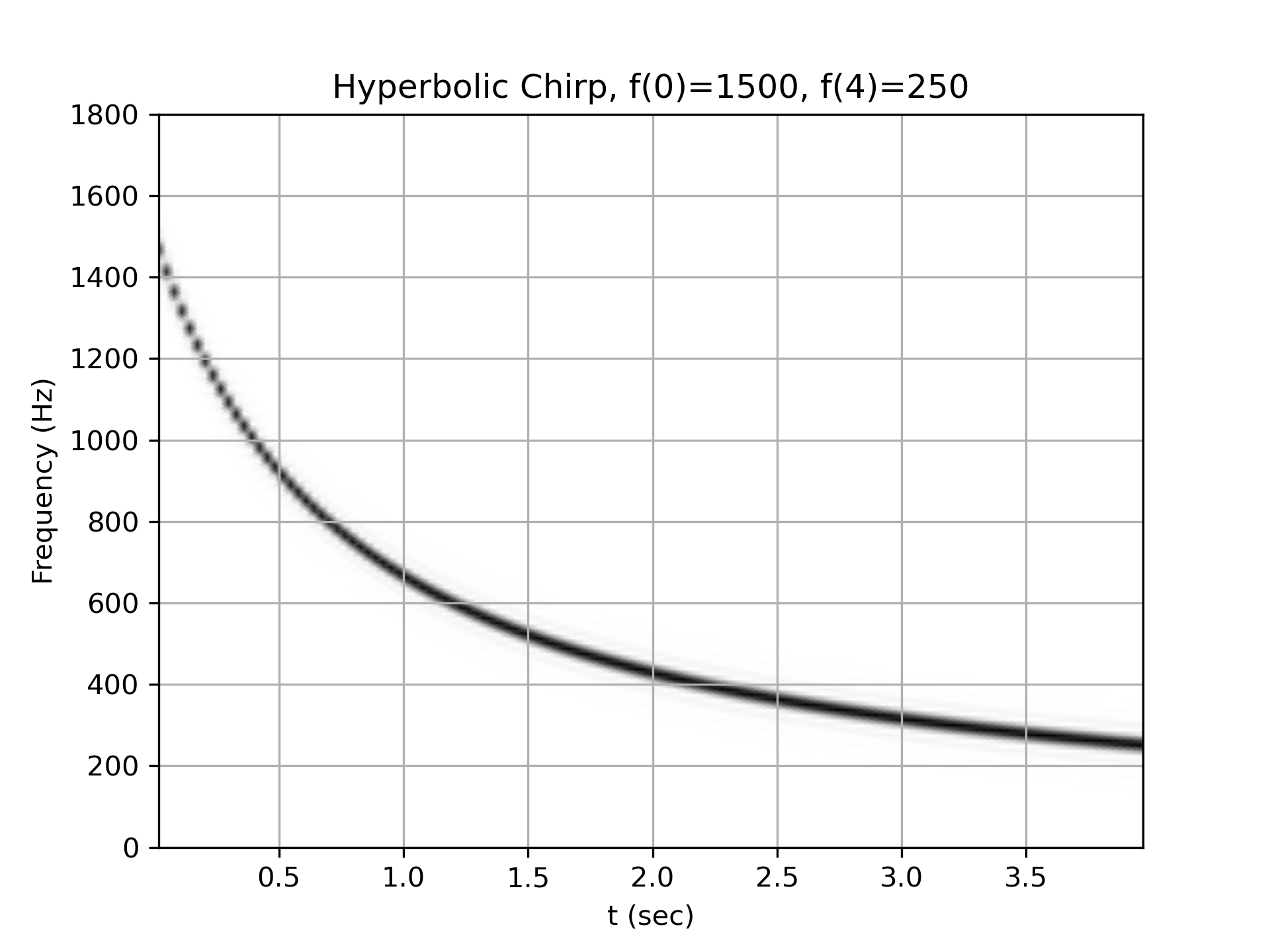
Hyperbolic chirp from 1500 Hz to 250 Hz:
>>> w = chirp(t, f0=1500, f1=250, t1=T, method='hyperbolic')
... plot_spectrogram(f'Hyperbolic Chirp, f(0)=1500, f({T})=250', w, fs)
... plt.show()
The following pages refer to to this document either explicitly or contain code examples using this.
scipy.signal._waveforms.chirp
scipy.signal._waveforms._chirp_phase
scipy.signal._waveforms.sweep_poly
scipy.signal._signaltools.hilbert
scipy.signal._peak_finding.peak_widths
Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.
Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)
SVG is more flexible but power hungry; and does not scale well to 50 + nodes.
All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them