gegenbauer(n, alpha, monic=False)
Defined to be the solution of
$$(1 - x^2)\frac{d^2}{dx^2}C_n^{(\alpha)} - (2\alpha + 1)x\frac{d}{dx}C_n^{(\alpha)} + n(n + 2\alpha)C_n^{(\alpha)} = 0$$for $\alpha > -1/2$ ; $C_n^{(\alpha)}$ is a polynomial of degree $n$ .
The polynomials $C_n^{(\alpha)}$ are orthogonal over $[-1,1]$ with weight function $(1 - x^2)^{(\alpha - 1/2)}$ .
Degree of the polynomial.
Parameter, must be greater than -0.5.
If :None:None:`True`, scale the leading coefficient to be 1. Default is :None:None:`False`.
Gegenbauer polynomial.
Gegenbauer (ultraspherical) polynomial.
>>> from scipy import special
... import matplotlib.pyplot as plt
We can initialize a variable p
as a Gegenbauer polynomial using the gegenbauer
function and evaluate at a point x = 1
.
>>> p = special.gegenbauer(3, 0.5, monic=False)
... p poly1d([ 2.5, 0. , -1.5, 0. ])
>>> p(1) 1.0
To evaluate p
at various points x
in the interval (-3, 3)
, simply pass an array x
to p
as follows:
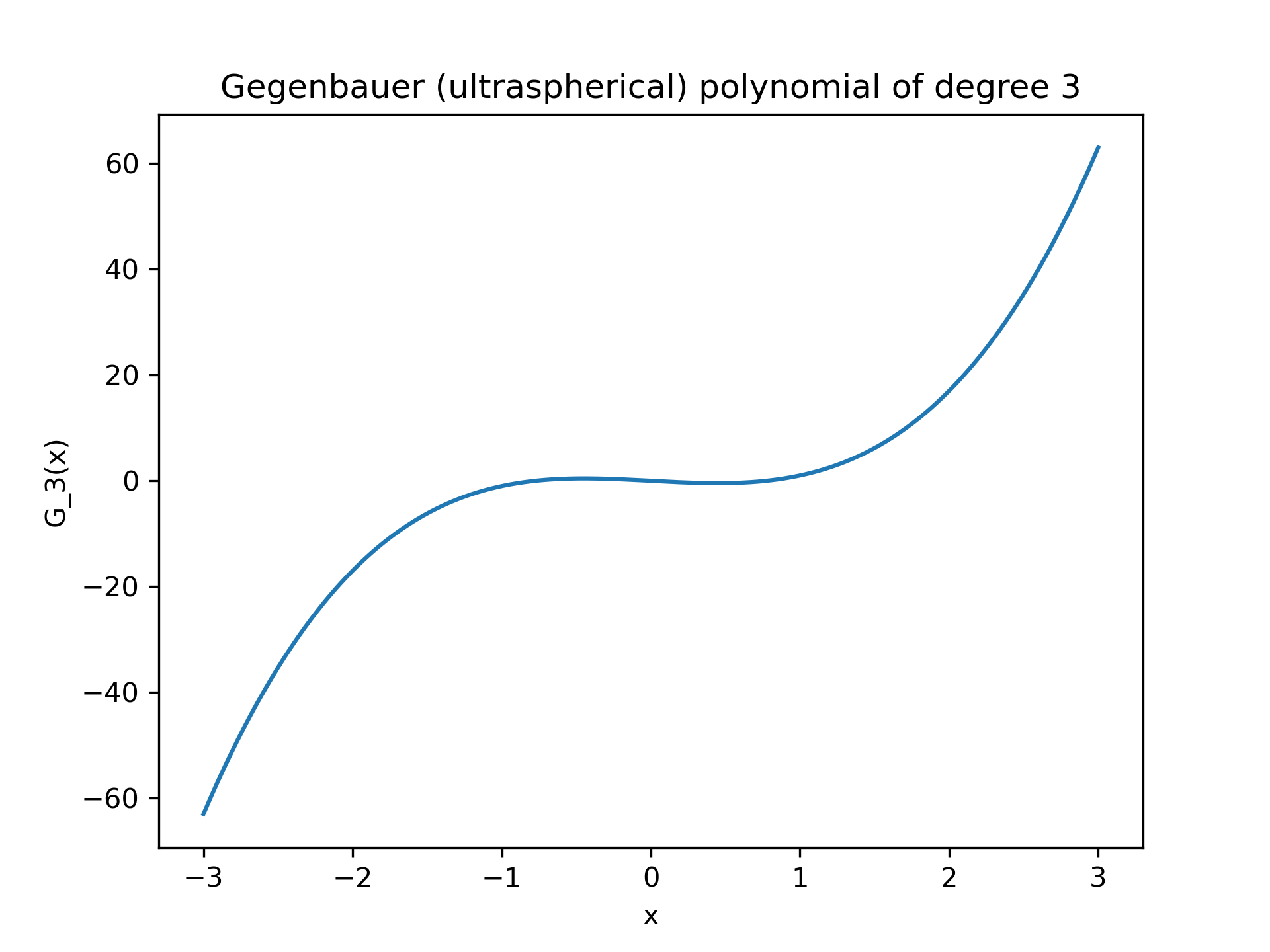
>>> x = np.linspace(-3, 3, 400)
... y = p(x)
We can then visualize x, y
using matplotlib.pyplot
.
>>> fig, ax = plt.subplots()
... ax.plot(x, y)
... ax.set_title("Gegenbauer (ultraspherical) polynomial of degree 3")
... ax.set_xlabel("x")
... ax.set_ylabel("G_3(x)")
... plt.show()
The following pages refer to to this document either explicitly or contain code examples using this.
scipy.special._orthogonal.gegenbauer
Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.
Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)
SVG is more flexible but power hungry; and does not scale well to 50 + nodes.
All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them