The rotation vectors between each consecutive orientation are cubic functions of time and it is guaranteed that angular rate and acceleration are continuous. Such interpolation are analogous to cubic spline interpolation.
Refer to for math and implementation details.
Times of the known rotations. At least 2 times must be specified.
Rotations to perform the interpolation between. Must contain N rotations.
Interpolate rotations with continuous angular rate and acceleration.
>>> from scipy.spatial.transform import Rotation, RotationSpline
Define the sequence of times and rotations from the Euler angles:
>>> times = [0, 10, 20, 40]
... angles = [[-10, 20, 30], [0, 15, 40], [-30, 45, 30], [20, 45, 90]]
... rotations = Rotation.from_euler('XYZ', angles, degrees=True)
Create the interpolator object:
>>> spline = RotationSpline(times, rotations)
Interpolate the Euler angles, angular rate and acceleration:
>>> angular_rate = np.rad2deg(spline(times, 1))
... angular_acceleration = np.rad2deg(spline(times, 2))
... times_plot = np.linspace(times[0], times[-1], 100)
... angles_plot = spline(times_plot).as_euler('XYZ', degrees=True)
... angular_rate_plot = np.rad2deg(spline(times_plot, 1))
... angular_acceleration_plot = np.rad2deg(spline(times_plot, 2))
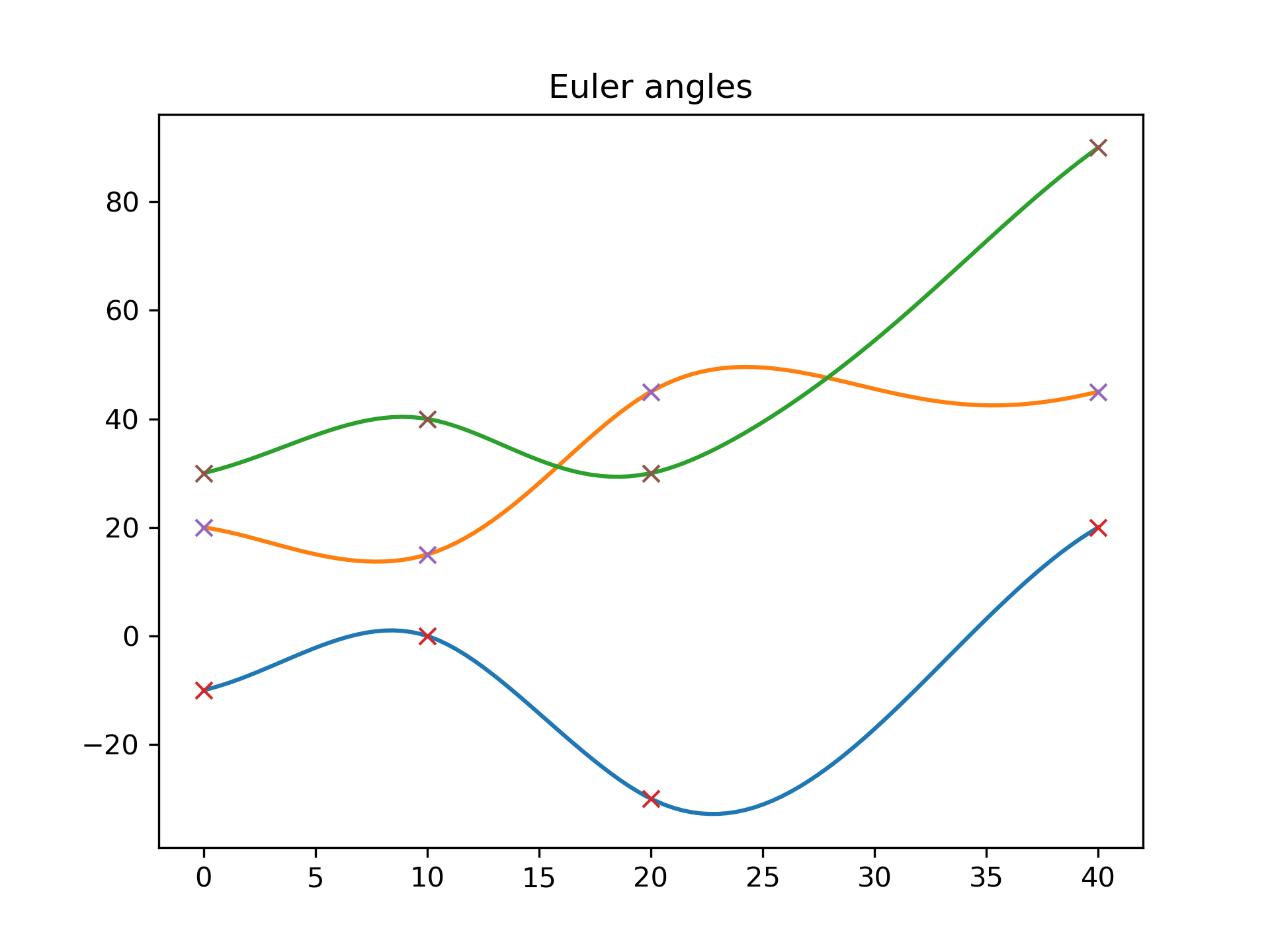
On this plot you see that Euler angles are continuous and smooth:
>>> import matplotlib.pyplot as plt
... plt.plot(times_plot, angles_plot)
... plt.plot(times, angles, 'x')
... plt.title("Euler angles")
... plt.show()
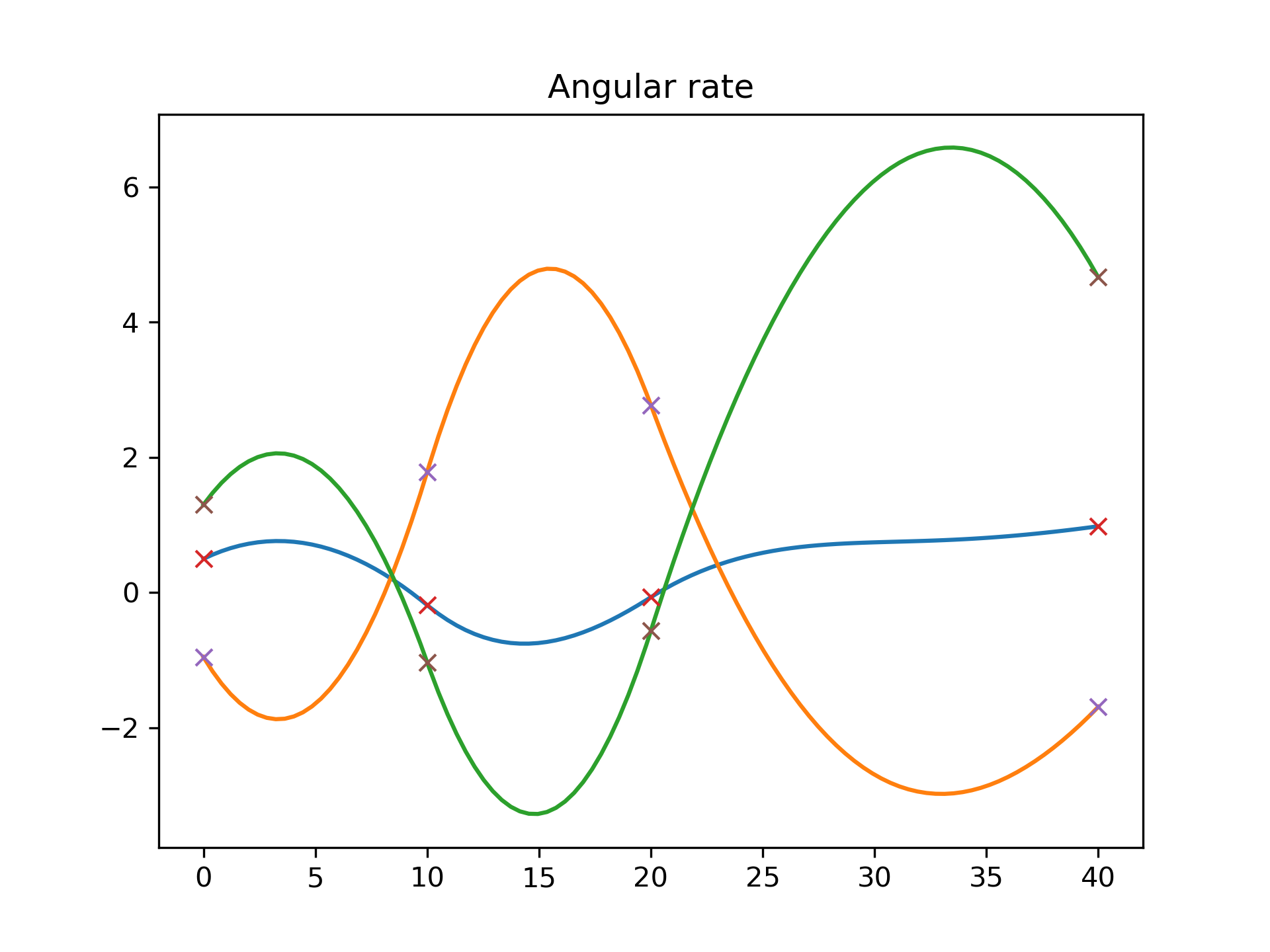
The angular rate is also smooth:
>>> plt.plot(times_plot, angular_rate_plot)
... plt.plot(times, angular_rate, 'x')
... plt.title("Angular rate")
... plt.show()
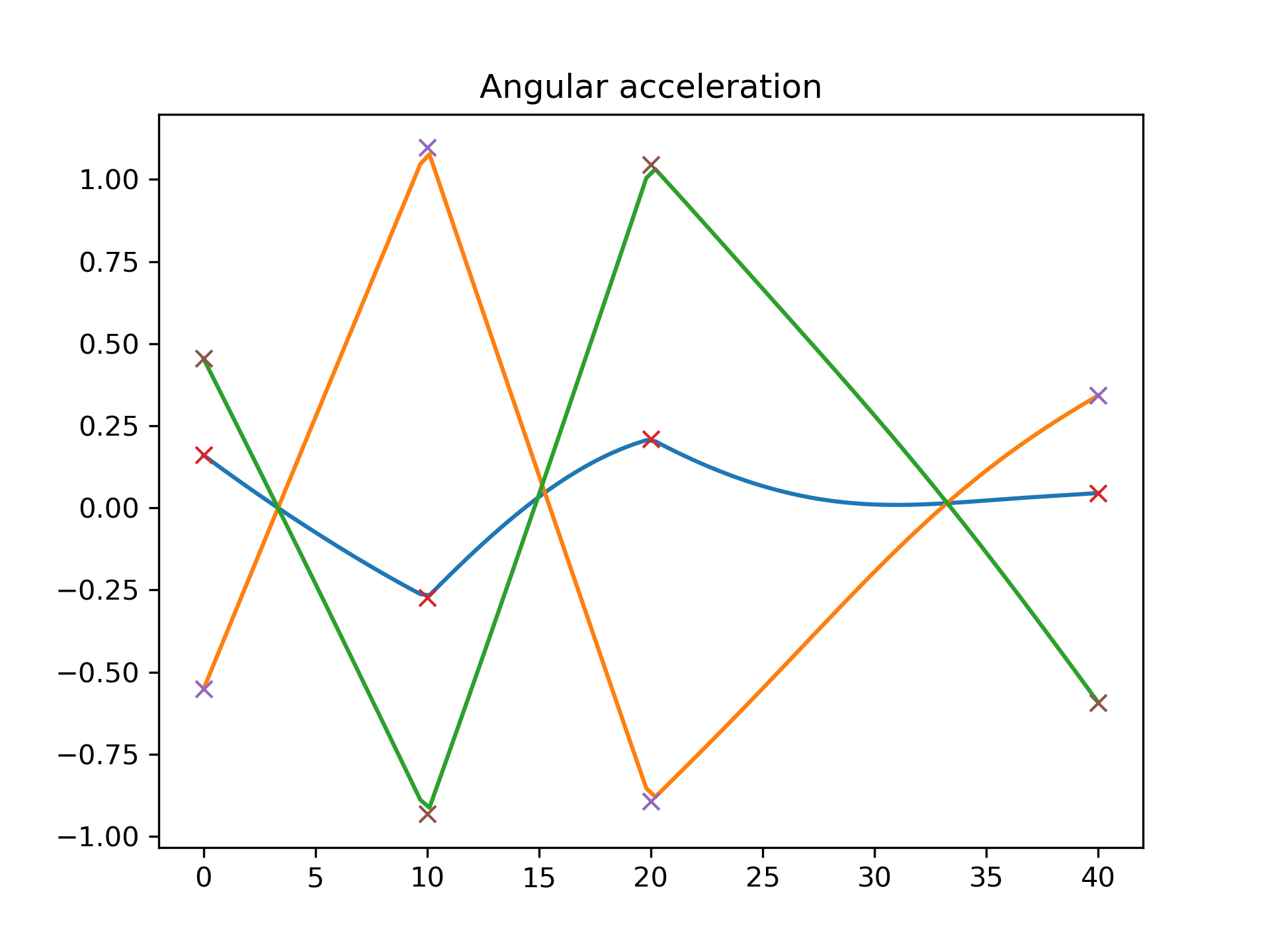
The angular acceleration is continuous, but not smooth. Also note that the angular acceleration is not a piecewise-linear function, because it is different from the second derivative of the rotation vector (which is a piecewise-linear function as in the cubic spline).
>>> plt.plot(times_plot, angular_acceleration_plot)
... plt.plot(times, angular_acceleration, 'x')
... plt.title("Angular acceleration")
... plt.show()
The following pages refer to to this document either explicitly or contain code examples using this.
scipy.spatial.transform._rotation_spline.RotationSpline
Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.
Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)
SVG is more flexible but power hungry; and does not scale well to 50 + nodes.
All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them