diric(x, n)

The Dirichlet function is defined as:

diric(x, n) = sin(x * n/2) / (n * sin(x / 2)),

where n is a positive integer.

Parameters

x : array_like

Input data

n : int

Integer defining the periodicity.

Returns

diric : ndarray

Periodic sinc function, also called the Dirichlet function.

Examples

>>> from scipy import special
... import matplotlib.pyplot as plt

>>> x = np.linspace(-8*np.pi, 8*np.pi, num=201)
... plt.figure(figsize=(8, 8));
... for idx, n in enumerate([2, 3, 4, 9]):
...     plt.subplot(2, 2, idx+1)
...     plt.plot(x, special.diric(x, n))
...     plt.title('diric, n={}'.format(n))
... plt.show()

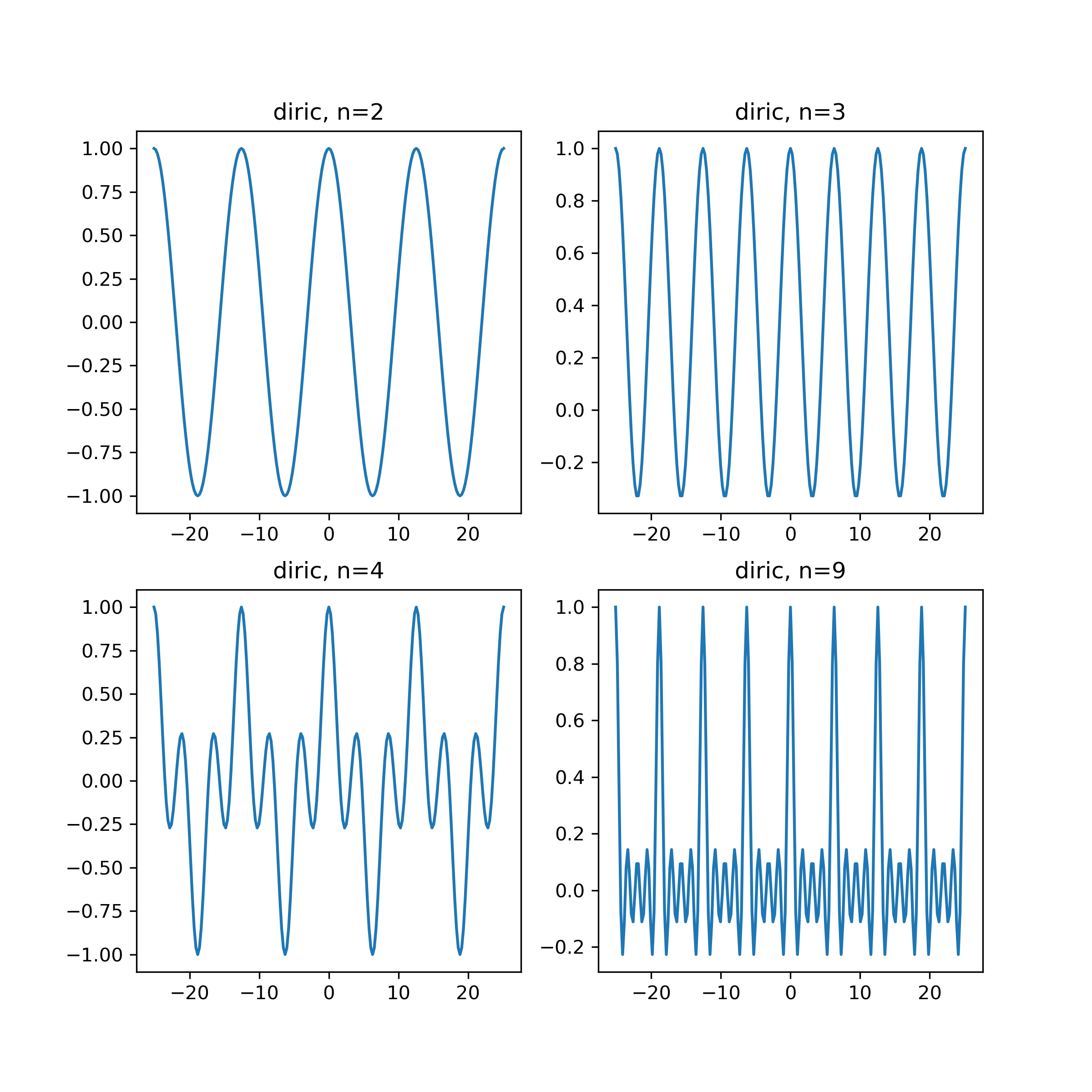
The following example demonstrates that diric gives the magnitudes (modulo the sign and scaling) of the Fourier coefficients of a rectangular pulse.

Suppress output of values that are effectively 0:

>>> np.set_printoptions(suppress=True)

Create a signal x of length :None:None:`m` with :None:None:`k` ones:

>>> m = 8
... k = 3
... x = np.zeros(m)
... x[:k] = 1

Use the FFT to compute the Fourier transform of x, and inspect the magnitudes of the coefficients:

>>> np.abs(np.fft.fft(x))
array([ 3.        ,  2.41421356,  1.        ,  0.41421356,  1.        ,
        0.41421356,  1.        ,  2.41421356])

Now find the same values (up to sign) using diric . We multiply by :None:None:`k` to account for the different scaling conventions of numpy.fft.fft and diric :

>>> theta = np.linspace(0, 2*np.pi, m, endpoint=False)
... k * special.diric(theta, k)
array([ 3.        ,  2.41421356,  1.        , -0.41421356, -1.        ,
       -0.41421356,  1.        ,  2.41421356])

See :

Back References

The following pages refer to to this document either explicitly or contain code examples using this.

scipy.special._basic.diric

Local connectivity graph

Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.

Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)

SVG is more flexible but power hungry; and does not scale well to 50 + nodes.

All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them

---

GitHub : /scipy/special/_basic.py#110
type: <class 'function'>
Commit: