curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=True, bounds=(-inf, inf), method=None, jac=None, **kwargs)
Assumes ydata = f(xdata, *params) + eps
.
With method='lm'
, the algorithm uses the Levenberg-Marquardt algorithm through leastsq
. Note that this algorithm can only deal with unconstrained problems.
Box constraints can be handled by methods 'trf' and 'dogbox'. Refer to the docstring of least_squares
for more information.
The model function, f(x, ...). It must take the independent variable as the first argument and the parameters to fit as separate remaining arguments.
The independent variable where the data is measured. Should usually be an M-length sequence or an (k,M)-shaped array for functions with k predictors, but can actually be any object.
The dependent data, a length M array - nominally f(xdata, ...)
.
Initial guess for the parameters (length N). If None, then the initial values will all be 1 (if the number of parameters for the function can be determined using introspection, otherwise a ValueError is raised).
Determines the uncertainty in ydata
. If we define residuals as r = ydata - f(xdata, *popt)
, then the interpretation of :None:None:`sigma` depends on its number of dimensions:
A 1-D
:None:None:`sigma`should contain values of standard deviations of errors inydata. In this case, the optimized function ischisq = sum((r / sigma) ** 2).A 2-D
:None:None:`sigma`should contain the covariance matrix of errors inydata. In this case, the optimized function ischisq = r.T @ inv(sigma) @ r.versionadded
None (default) is equivalent of 1-D :None:None:`sigma` filled with ones.
If True, :None:None:`sigma` is used in an absolute sense and the estimated parameter covariance :None:None:`pcov` reflects these absolute values.
If False (default), only the relative magnitudes of the :None:None:`sigma` values matter. The returned parameter covariance matrix :None:None:`pcov` is based on scaling :None:None:`sigma` by a constant factor. This constant is set by demanding that the reduced :None:None:`chisq` for the optimal parameters :None:None:`popt` when using the scaled :None:None:`sigma` equals unity. In other words, :None:None:`sigma` is scaled to match the sample variance of the residuals after the fit. Default is False. Mathematically, pcov(absolute_sigma=False) = pcov(absolute_sigma=True) * chisq(popt)/(M-N)
If True, check that the input arrays do not contain nans of infs, and raise a ValueError if they do. Setting this parameter to False may silently produce nonsensical results if the input arrays do contain nans. Default is True.
Lower and upper bounds on parameters. Defaults to no bounds. Each element of the tuple must be either an array with the length equal to the number of parameters, or a scalar (in which case the bound is taken to be the same for all parameters). Use np.inf
with an appropriate sign to disable bounds on all or some parameters.
Method to use for optimization. See least_squares
for more details. Default is 'lm' for unconstrained problems and 'trf' if :None:None:`bounds` are provided. The method 'lm' won't work when the number of observations is less than the number of variables, use 'trf' or 'dogbox' in this case.
Function with signature jac(x, ...)
which computes the Jacobian matrix of the model function with respect to parameters as a dense array_like structure. It will be scaled according to provided :None:None:`sigma`. If None (default), the Jacobian will be estimated numerically. String keywords for 'trf' and 'dogbox' methods can be used to select a finite difference scheme, see least_squares
.
Keyword arguments passed to leastsq
for method='lm'
or least_squares
otherwise.
if either ydata
or :None:None:`xdata` contain NaNs, or if incompatible options are used.
if the least-squares minimization fails.
if covariance of the parameters can not be estimated.
Optimal values for the parameters so that the sum of the squared residuals of f(xdata, *popt) - ydata
is minimized.
The estimated covariance of popt. The diagonals provide the variance of the parameter estimate. To compute one standard deviation errors on the parameters use perr = np.sqrt(np.diag(pcov))
.
How the :None:None:`sigma` parameter affects the estimated covariance depends on :None:None:`absolute_sigma` argument, as described above.
If the Jacobian matrix at the solution doesn't have a full rank, then 'lm' method returns a matrix filled with np.inf
, on the other hand 'trf' and 'dogbox' methods use Moore-Penrose pseudoinverse to compute the covariance matrix.
Use non-linear least squares to fit a function, f, to data.
least_squares
Minimize the sum of squares of nonlinear functions.
scipy.stats.linregress
Calculate a linear least squares regression for two sets of measurements.
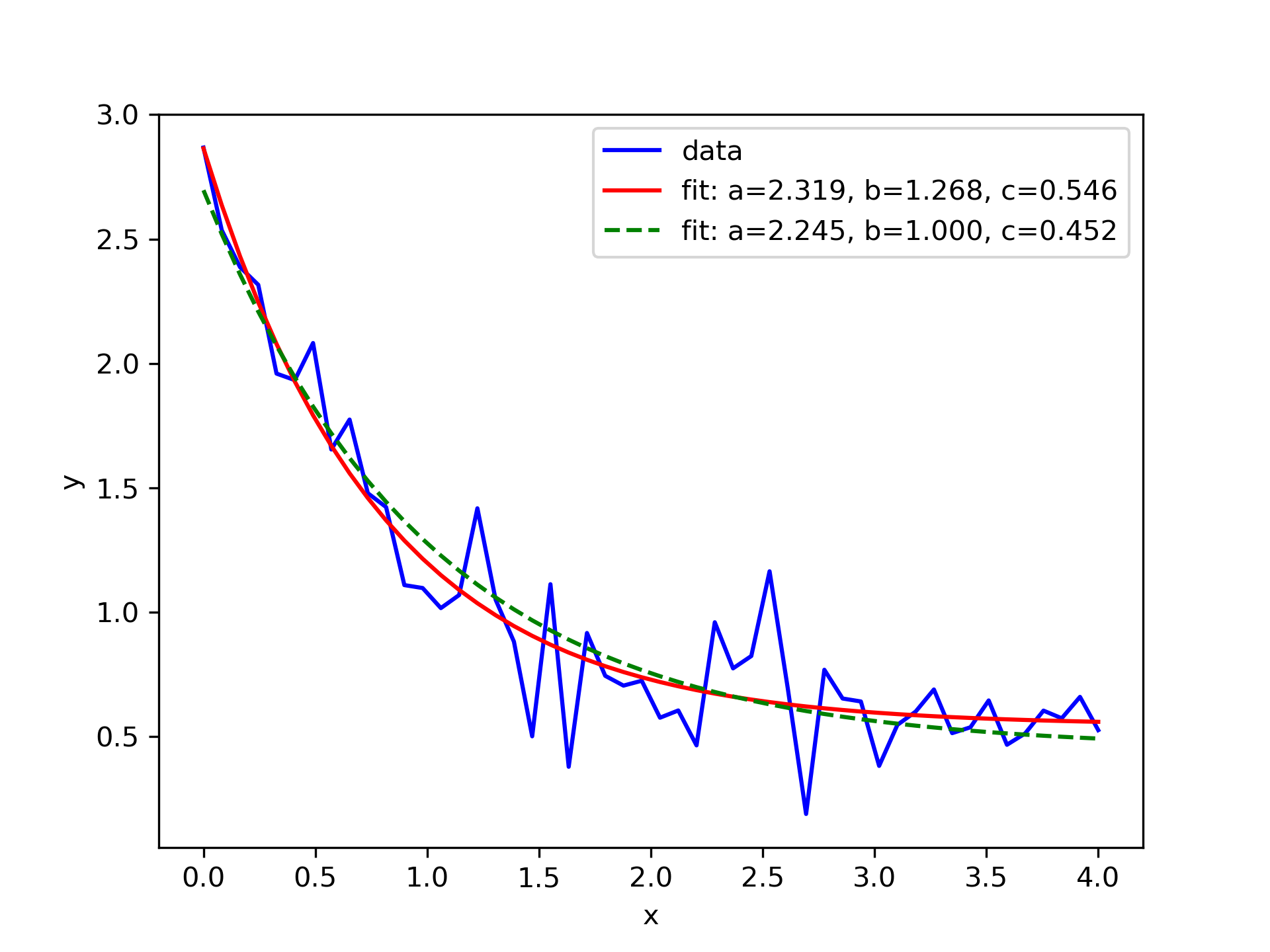
>>> import matplotlib.pyplot as plt
... from scipy.optimize import curve_fit
>>> def func(x, a, b, c):
... return a * np.exp(-b * x) + c
Define the data to be fit with some noise:
>>> xdata = np.linspace(0, 4, 50)
... y = func(xdata, 2.5, 1.3, 0.5)
... rng = np.random.default_rng()
... y_noise = 0.2 * rng.normal(size=xdata.size)
... ydata = y + y_noise
... plt.plot(xdata, ydata, 'b-', label='data')
Fit for the parameters a, b, c of the function :None:None:`func`:
>>> popt, pcov = curve_fit(func, xdata, ydata)
... popt array([2.56274217, 1.37268521, 0.47427475])
>>> plt.plot(xdata, func(xdata, *popt), 'r-',
... label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
Constrain the optimization to the region of 0 <= a <= 3
, 0 <= b <= 1
and 0 <= c <= 0.5
:
>>> popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5]))
... popt array([2.43736712, 1. , 0.34463856])
>>> plt.plot(xdata, func(xdata, *popt), 'g--',
... label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
>>> plt.xlabel('x')
... plt.ylabel('y')
... plt.legend()
... plt.show()
The following pages refer to to this document either explicitly or contain code examples using this.
scipy.optimize._minpack_py.curve_fit
Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.
Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)
SVG is more flexible but power hungry; and does not scale well to 50 + nodes.
All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them