interp2d(x, y, z, kind='linear', copy=True, bounds_error=False, fill_value=None)
x, y and z are arrays of values used to approximate some function f: z = f(x, y)
which returns a scalar value z. This class returns a function whose call method uses spline interpolation to find the value of new points.
If x and y represent a regular grid, consider using RectBivariateSpline
.
If z is a vector value, consider using interpn
.
Note that calling interp2d
with NaNs present in input values results in undefined behaviour.
The minimum number of data points required along the interpolation axis is (k+1)**2
, with k=1 for linear, k=3 for cubic and k=5 for quintic interpolation.
The interpolator is constructed by bisplrep
, with a smoothing factor of 0. If more control over smoothing is needed, bisplrep
should be used directly.
Arrays defining the data point coordinates.
If the points lie on a regular grid, x can specify the column coordinates and y the row coordinates, for example:
>>> x = [0,1,2]; y = [0,3]; z = [[1,2,3], [4,5,6]]
Otherwise, x and y must specify the full coordinates for each point, for example:
>>> x = [0,1,2,0,1,2]; y = [0,0,0,3,3,3]; z = [1,2,3,4,5,6]
If x and y are multidimensional, they are flattened before use.
The values of the function to interpolate at the data points. If z is a multidimensional array, it is flattened before use. The length of a flattened z array is either len(x)*len(y) if x and y specify the column and row coordinates or len(z) == len(x) == len(y)
if x and y specify coordinates for each point.
The kind of spline interpolation to use. Default is 'linear'.
If True, the class makes internal copies of x, y and z. If False, references may be used. The default is to copy.
If True, when interpolated values are requested outside of the domain of the input data (x,y), a ValueError is raised. If False, then :None:None:`fill_value` is used.
If provided, the value to use for points outside of the interpolation domain. If omitted (None), values outside the domain are extrapolated via nearest-neighbor extrapolation.
Interpolate over a 2-D grid.
BivariateSpline
a more recent wrapper of the FITPACK routines
RectBivariateSpline
Much faster 2-D interpolation if your input data is on a grid
bisplev
Spline interpolation based on FITPACK
bisplrep
Spline interpolation based on FITPACK
interp1d
1-D version of this function
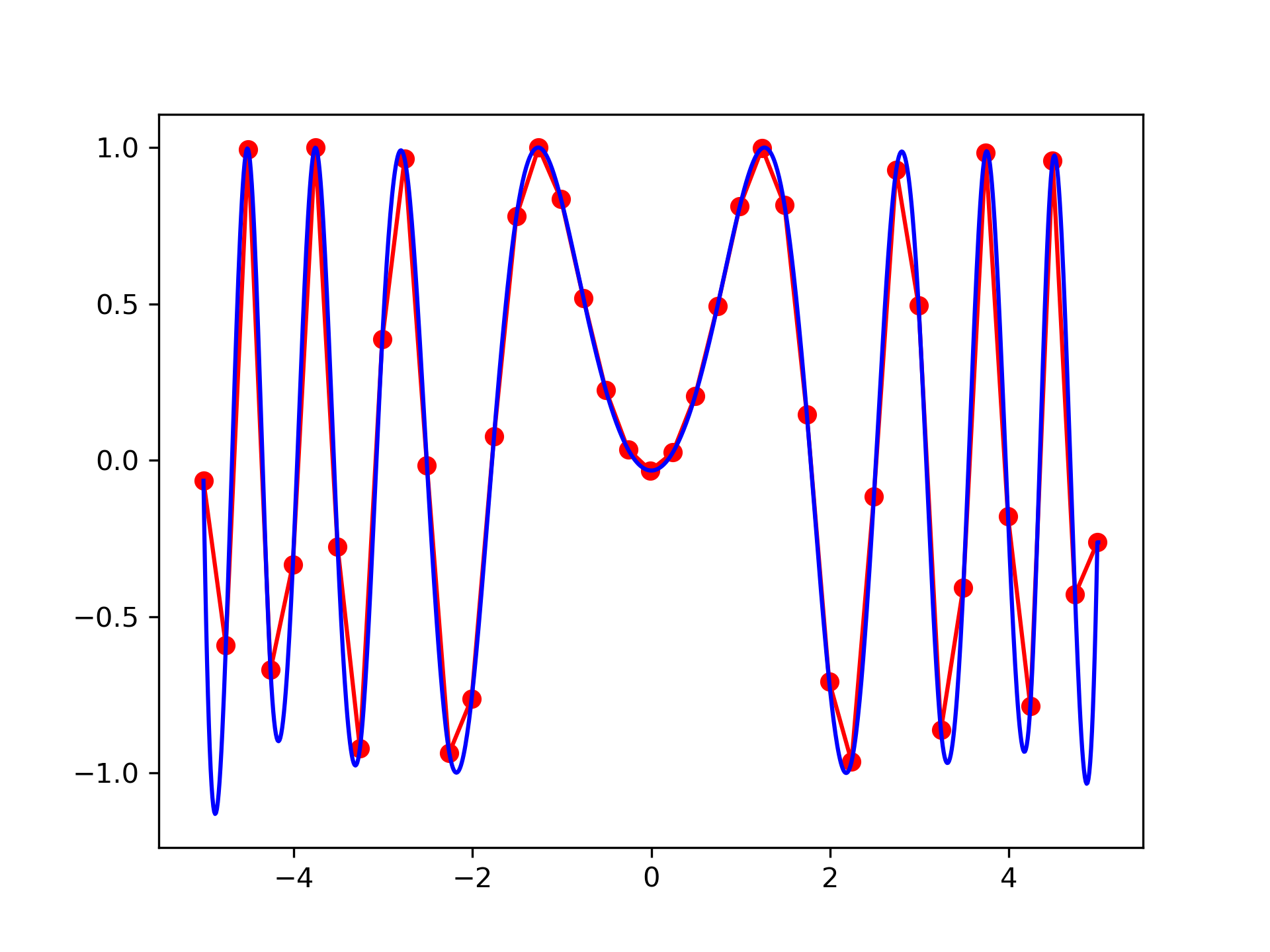
Construct a 2-D grid and interpolate on it:
>>> from scipy import interpolate
... x = np.arange(-5.01, 5.01, 0.25)
... y = np.arange(-5.01, 5.01, 0.25)
... xx, yy = np.meshgrid(x, y)
... z = np.sin(xx**2+yy**2)
... f = interpolate.interp2d(x, y, z, kind='cubic')
Now use the obtained interpolation function and plot the result:
>>> import matplotlib.pyplot as plt
... xnew = np.arange(-5.01, 5.01, 1e-2)
... ynew = np.arange(-5.01, 5.01, 1e-2)
... znew = f(xnew, ynew)
... plt.plot(x, z[0, :], 'ro-', xnew, znew[0, :], 'b-')
... plt.show()
The following pages refer to to this document either explicitly or contain code examples using this.
scipy.interpolate._interpolate.interp2d
scipy.interpolate._interpolate.interp1d
Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.
Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)
SVG is more flexible but power hungry; and does not scale well to 50 + nodes.
All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them