quad_vec(f, a, b, epsabs=1e-200, epsrel=1e-08, norm='2', cache_size=100000000.0, limit=10000, workers=1, points=None, quadrature=None, full_output=False, *, args=())
The algorithm mainly follows the implementation of QUADPACK's DQAG* algorithms, implementing global error control and adaptive subdivision.
The algorithm here has some differences to the QUADPACK approach:
Instead of subdividing one interval at a time, the algorithm subdivides N intervals with largest errors at once. This enables (partial) parallelization of the integration.
The logic of subdividing "next largest" intervals first is then not implemented, and we rely on the above extension to avoid concentrating on "small" intervals only.
The Wynn epsilon table extrapolation is not used (QUADPACK uses it for infinite intervals). This is because the algorithm here is supposed to work on vector-valued functions, in an user-specified norm, and the extension of the epsilon algorithm to this case does not appear to be widely agreed. For max-norm, using elementwise Wynn epsilon could be possible, but we do not do this here with the hope that the epsilon extrapolation is mainly useful in special cases.
Vector-valued function f(x) to integrate.
Initial point.
Final point.
Absolute tolerance.
Relative tolerance.
Vector norm to use for error estimation.
Number of bytes to use for memoization.
If :None:None:`workers` is an integer, part of the computation is done in parallel subdivided to this many tasks (using python:multiprocessing.pool.Pool
). Supply :None:None:`-1` to use all cores available to the Process. Alternatively, supply a map-like callable, such as python:multiprocessing.pool.Pool.map
for evaluating the population in parallel. This evaluation is carried out as workers(func, iterable)
.
List of additional breakpoints.
Quadrature rule to use on subintervals. Options: 'gk21' (Gauss-Kronrod 21-point rule), 'gk15' (Gauss-Kronrod 15-point rule), 'trapezoid' (composite trapezoid rule). Default: 'gk21' for finite intervals and 'gk15' for (semi-)infinite
Return an additional info
dictionary.
Extra arguments to pass to function, if any.
Estimate for the result
Error estimate for the result in the given norm
Returned only when full_output=True
. Info dictionary. Is an object with the attributes:
success
success
status
status
neval
neval
intervals
intervals
integrals
integrals
errors
errors
Adaptive integration of a vector-valued function.
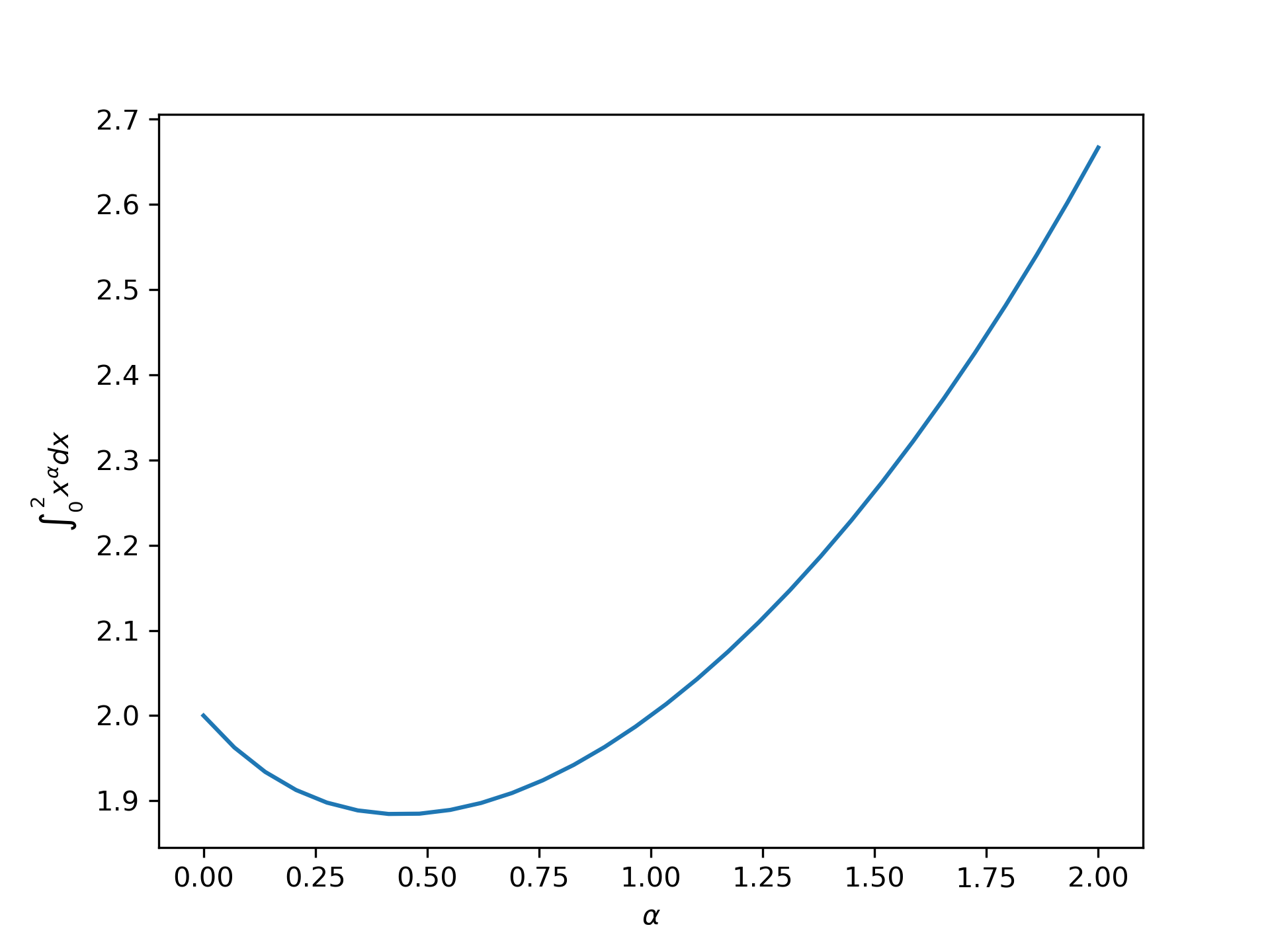
We can compute integrations of a vector-valued function:
>>> from scipy.integrate import quad_vec
... import matplotlib.pyplot as plt
... alpha = np.linspace(0.0, 2.0, num=30)
... f = lambda x: x**alpha
... x0, x1 = 0, 2
... y, err = quad_vec(f, x0, x1)
... plt.plot(alpha, y)
... plt.xlabel(r"$\alpha$")
... plt.ylabel(r"$\int_{0}^{2} x^\alpha dx$")
... plt.show()
The following pages refer to to this document either explicitly or contain code examples using this.
scipy.integrate._quad_vec.quad_vec
Hover to see nodes names; edges to Self not shown, Caped at 50 nodes.
Using a canvas is more power efficient and can get hundred of nodes ; but does not allow hyperlinks; , arrows or text (beyond on hover)
SVG is more flexible but power hungry; and does not scale well to 50 + nodes.
All aboves nodes referred to, (or are referred from) current nodes; Edges from Self to other have been omitted (or all nodes would be connected to the central node "self" which is not useful). Nodes are colored by the library they belong to, and scaled with the number of references pointing them